Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 20

Пусть  и  - базисные векторы прямоугольной декартовой системы координат. Так как , то в силу дистрибутивности (свойство 6) получим: . На основании свойства 4 далее имеем: . Но по определению скалярного произведения (или в силу свойств 2 и 3) , поэтому последнее выражение скалярного произведения совпадает с (2.7.8).

Полученное выражение скалярного произведения через координаты позволяет решить следующие задачи.

Задача 1. Найти длину вектора .

Решение. По свойству 2 им формуле (2.7.8) . Отсюда следует, что длина вектора равна корню квадратному из суммы квадратов его координат:

                                         (2.7.9)

Из полученной формулы можно еще раз получить формулу расстояния между двумя точками (1.2.1). если А(х₁, у₁), и В(х₂, у₂), то  и по формуле (2.7.8) получаем .

Задача 2. Найти угол между векторами  и .

Решение. По определению скалярного произведения и формулам (2.7.8) и (2.7.9) имеем:

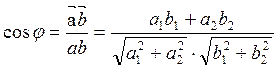             (2.7.10)

Пример. Найдите острый угол между медианами катетов прямоугольного равнобедренного треугольника.

          Решение. Пусть в треугольнике АВС медианы катетов обозначены АА₁ и ВВ₁ (рис. 2.25). Требуется найти угол φ, представляющий собой угол между векторами и                                                                       у

                                                                                            В

                                                       

                                                     ·    Φ                              А₁

    ·      φ                             πφ                                              _φ

                                                                                         С                                  х

В₁            А                   

Рис. 2.23                            Рис. 2.24                                         Рис. 2.25

Введем систему координат, полагая вершину С прямого угла началом координат, а отрезки СА₁ и СВ₁ – единичными отрезками осей. Тогда В₁(1, 0), А(2, 0), А₁(0, 1), В(0, 2) и, следовательно, . Теперь по формуле угла между векторами (2.7.10) 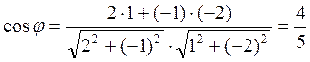 откуда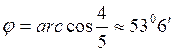

Глава 3. ПРЯМАЯ

§ 3.1. Уравнение прямой по точке и направляющему вектору,

 по точке и нормальному вектору

Определение. Ненулевой вектор называется направляющим вектором прямой, если он ей параллелен или лежит на ней.

Всякая прямая имеет бесконечное множество направляющих векторов, но они все коллинеарны. Значит, если  - направляющий вектор прямой, то всякий направляющий вектор этой прямой можно записать в виде , где .

Точка, принадлежащая прямой, и направляющий вектор этой прямой определяют прямую. Поэтому следующая задача имеет единственное решение.

Задача 1. Найти уравнение прямой  по точке А(х₀, у₀) и направляющему вектору .

Решение. Пусть М(х, у) – какая-либо точка (рис. 3.1). Тогда  и 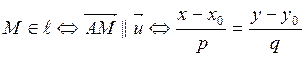. Мы получили уравнение прямой по точке и направляющему вектору:

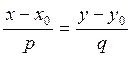                                     (3.1.1)

Полученным уравнением можно пользоваться и тогда, когда одно из чисел p или q равно нулю. Надо только помнить, что говорилось о делении на нуль в § 2.5.

Допустим, требуется найти уравнение прямой по точке А(2, 1) и направляющему вектору , смотри рис. 3.2. По формуле (3.1.1) получаем 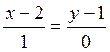. Правая часть этого уравнения имеет смысл только при у-1=0. Но тогда уравнение 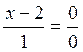 можно считать тождеством,

                                                                         у     у-1=0        А          

                                                                                                   ·          

                                     М

· А                                                           о                          х

 

Рис. 3.1                                                        Рис. 3.2

так как правая часть равна любому числу. Следовательно, у-1=0 и есть уравнение искомой прямой.

Исходя из уравнения (3.1.1), можно получить еще два полезных вида уравнения прямой.