Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 14

В самом деле, на том же рис. 2.10 , а векторы  и  противоположны.

Свойство 6. Чтобы вычесть вектор, достаточно прибавить противоположный:

                                     (2.2.10)

Действительно,  и потому .

                                     С            А                 В                                   А

      А

                                                                   

                                  О                                                                     В

                               В                                    С               О         

О                                                                                                           

Рис. 2.8                                Рис. 2.9                                    Рис. 2.10

Свойство 7. При прибавлении суммы и разности векторов действуют те же правила раскрытия скобок (и заключения в скобки), что и для действительных чисел:

                                       (2.2.11)

Первое из этих равенств есть уже доказанное ранее ассоциативность сложения (2.2.8). Второе доказывается с применением свойств 6 и ассоциативности:

Оставшиеся две формулы доказываются в таком же стиле. Читателю полезно выполнить все рассуждения.

Свойство 8. Модуль разности двух векторов не превосходит сумму их модулей:

                                        (2.2.12)

Для доказательства воспользуемся свойствами 6 и 1:

Читателю предлагается самостоятельно конкретизировать это свойство по аналогии со свойством 1.

§ 2.3. Умножение вектора на число

Определение. Произведением вектора  на действительное число λ называется вектор ,определяемый двумя условиями: а) если λ>0, то ; если λ<0, то .

б) длина вектора  равна длине вектора , умноженной на абсолютную величину числа λ: .

Обозначение произведения вектора на число: . Из определения, в частности, следует, что если λ=0 или , то , и наоборот.

Теорема. (Бескоординатным признак коллинеарности векторов). Для того, чтобы вектор  и ненулевой вектор  были коллинеарны, необходимо и достаточно, чтобы существовало действительное число λ, удовлетворяющее условию .

Условие теоремы удобно представить в следующем виде:

.

Доказательство. Достаточность (на схеме буква «Д») вытекает из определения умножения вектора на число. Необходимость (на схеме буква «Н»). Даны два коллинеарных вектора  и , причем . Если , то теорема верна, так как при λ=0 равенство  выполняется. Поэтому в дальнейшем считаем . Положим .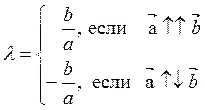

Убедимся, что при так выбранном λ будет . Для этого надо доказать равенство длин и сонаправленность векторов  и . Сонаправленность:

При  будет λ>0 и ,

При  будет λ<0 и .

Равенство длин: .

Таким образом. Число λ, удовлетворяющее условию теоремы, существует. Теорема доказана.

Пользуясь понятием умножения вектора на число, можно ввести понятие деления коллинеарных векторов. А именно, если || и , то по доказанной теореме существует λ такое, что . Это λ и называют отношением вектора  к вектору . Запись: 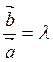. Еще раз подчеркиваем, что понятие деления имеет смысл только  для коллинеарных векторов.

Далее рассмотрим свойства умножения вектора на число.

Свойство 1. Для любых действительных чисел λ, μ и любого вектора  верно равенство

                                      (2.3.1)

Доказательство. Если либо λ=0, либо μ=0, либо , то свойство выполняется тривиальным образом. Поэтому далее считаем, что нулевых сомножителей нет. Если обозначить  и , то надо доказать равенство векторов  и , то есть требуется доказать равенство их длин u=v и сонаправленность .

Равенство длин:

.

Равенства 1, 2. 3 верны в силу определения умножения вектора на  число, а равенство 4 – потому, что модуль произведения чисел равен произведению их модулей.

Для доказательства сонаправленности нужно рассмотреть все возможные комбинации знаков λ и μ:

1.  λ>0, μ>0,         2. λ>0, μ<0,          3. λ<0, μ>0,          4. λ<0, μ<0