Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 16

Получили  или . Из последнего равенства с учетом того, что . Получаем: 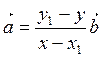, откуда , что противоречит условию. Теорема доказана полностью.

Зададим на плоскости аффинную систему координат: О – начало, ОЕ₁ и ОЕ₂ – единичные отрезки на осях (рис. 2.14). Положим . Мы видим. Что аффинную систему координат можно задать началом и парой произвольных неколлинеарных  векторов  и , которые называются координатными или базисными.

Определение. Координатами вектора называются коэффициенты в разложении этого вектора по базисным векторам.

По теореме 1 всякий вектор  можно единственным образом разложить по базисным векторам, то есть представить в виде . Коэффициенты х, у и есть координаты вектора , что записывается так:  или .

Определение. Вектор , где О начало координат. Называется радиус-вектором точки М.

Пусть . Если проследить ход разложения вектора  по базисным векторам (такие рассуждения подробно описаны в ходе доказательства теоремы 1), то ясно, что х, у – это координаты точки М. Мы приходим к выводу: координаты радиус-вектора равны координатам его конца.

Теорема 2. При сложении (вычитании) векторов их соответствующие координаты складываются (вычитаются). При умножении вектора на число их координаты умножаются на это число.

Дано:

Требуется доказать: .

Доказательство. Имеем:

.

Здесь равенство 1 построено на основании первого дистрибутивного закона (§ 2.3, свойство 2), ассоциативности и коммутативности сложения векторов (§ 2.2, свойства 3, 4). Равенство 2 поставлено на основании свойства 2 и 1, § 2.3. Теорема доказана.

Теорема 3. Координаты вектора равны разностям между соответствующими координатами его концов.

Дано: А(х₁, у₁), В(х₂, у₂) (рис. 2.15).

Требуется доказать:

 

             В                                    у                                        у      А                        В

                   М₂            М

                                                           Е₂

                                        

                                                             О     Е₁

    О                 А     М₁                                           х               О                         х

Рис. 2.13                                            Рис. 2.14                                   Рис. 2.15

Доказательство. По определению вычитания векторов будет . Так как  и  - радиус-векторы, то их координаты равны координатам их концов:  Теперь по теореме 2 имеем , что и требовалось доказать.

Пример. Даны координаты трех вершин параллелограмма АВСD: А(1, 2), В(-3, 4), С(-1, 2). Найдите координаты четвертой вершины.

Решение. Обозначим D(х, у). По теореме 3 имеем: . Но так как , то 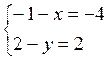, откуда х=3, у=0. Итак, D(3, 0).

§ 2.5. Коллинеарность векторов в координатах. Применение векторов

к выводу формул аналитической геометрии

Определение.  Две упорядоченные пары чисел (а₁, а₂) и (, ) называются пропорциональными, если существует число λ такое, что при умножении на него чисел одной пары получаются числа другой, например,

                                 (2.5.1)

Условие пропорциональности чаще записывают при помощи деления:

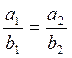                                               (2.5.2)

Оба эти условия в случае, когда элементы пар отличны от нуля, эквивалентны. Но когда в парах есть нули, условие (2.5.2) может потерять смысл. Однако, если принять во внимание, что дробь  при  не существует (деление на нуль невозможно), а дробь  можно считать равной любому числу (то есть в этом случае деление на нуль возможно, но не однозначно), то условием (2.5.2) можно пользоваться во всех случаях. Поясним это двумя примерами.

1). Пары (1, 0) и (0, 3) не пропорциональны, так как равенства 1=λ·0, 0=λ·3, так же как и равенства 0=μ·1, 3=μ·0, не выполняются ни при каких λ и μ.

Применяя (2.5.2) получаем две дроби:  и . Первая из них не существует, поэтому   . Мы пришли к тому же выводу.