F(х, у) = 0 (1.3.2)
Пример 3. Уравнение х-у=0 равносильно уравнению из примера 1, поэтому оно является уравнением прямой.
Пример 4. Уравнение х2+у2-1=0. Из формулы (1.2.2) ясно, что ему удовлетворяют координаты точек, лежащих на окружности радиуса 1 с центром в начале координат (рис. 1.12).
![]()
![]() у у
у
у у
у
![]()
![]()
![]()
 М(х,
у)
М(х,
у)
 у
у
![]()
![]()
![]()
![]()
![]() у М(х, у) у М(х, у)
· х о х
у М(х, у) у М(х, у)
· х о х
![]() о · х
о · х
![]() х
о х х
х
о х х
Рис. 1.10 Рис. 1.11 Рис. 1.12
![]() Пример 5.
Уравнение х2+у2=0
удовлетворяет только одна пара действительных чисел – (0, 0). Следовательно, в
данном случае линия вырождается в точку.
Пример 5.
Уравнение х2+у2=0
удовлетворяет только одна пара действительных чисел – (0, 0). Следовательно, в
данном случае линия вырождается в точку.
Пример 6. Уравнению х2+у2+1=0 не удовлетворяет ни одна пара действительных чисел, следовательно, линия вырождается в пустое множество.
Из приведенных примеров видим, что уравнение (1.3.2) не всегда определяет линию; будем говорить, что оно, вообще говоря, определяет некоторую линию.
Вывод: множество всех точек, координаты которых удовлетворяют уравнению (1.3.2), представляет собой, вообще говоря, некоторую линию; само уравнение называется уравнением этой линии.
Уравнение линии выражает зависимость между координатами произвольной (или текущей) точки данной линии. Переменные координаты, входящие в уравнение, называются текущими координатами.
Зависимость между текущими координатами может быть задана и в другой форме – параметрической, если обе текущие координаты выразить через новую переменную, называемую параметром. Общий вид параметрических уравнений такой:
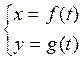 (1.3.3)
(1.3.3)
где t – параметр. Если из этих уравнений каким-либо способом исключить параметр (например, из первого уравнения выразить t через х и подставить во второе), то придем к уравнению вида (1.3.1) или (1.3.2). Этому уравнению удовлетворяют координаты всех точек линии (1.3.3). Следовательно, если линия задана параметрически и из параметрических уравнений исключить параметр, то получим уравнение новой кривой, которая либо совпадает с данной линией, либо содержит ее как часть.
Пример
7. Параметрические уравнения 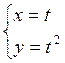 , при
исключении параметра t приводят
к уравнению параболы у=х
, при
исключении параметра t приводят
к уравнению параболы у=х![]() , причем для каждой
точки параболы можно подобрать соответствующее значение параметра. Значит,
данные параметрические уравнения определяют параболу.
, причем для каждой
точки параболы можно подобрать соответствующее значение параметра. Значит,
данные параметрические уравнения определяют параболу.
Пример 8. Параметрические
уравнения 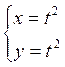 при исключении параметра t
приводят к уравнению у=х – уравнению биссектрисы I и IIIкоординатных
углов. Однако данные параметрические уравнения определяют не всю биссектрису, а
только ее часть, находящуюся в I координатном углу, так как х=у=t2
при исключении параметра t
приводят к уравнению у=х – уравнению биссектрисы I и IIIкоординатных
углов. Однако данные параметрические уравнения определяют не всю биссектрису, а
только ее часть, находящуюся в I координатном углу, так как х=у=t2![]() 0/
0/
В настоящем параграфе изложена основная идея метода аналитической геометрии. Мы можем теперь изучение свойств линий заменить изучением свойств их уравнений, а также и наоборот. Наиболее естественно решаются вопросы, связанные с пересечением двух линий.
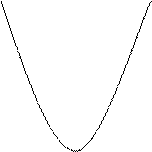
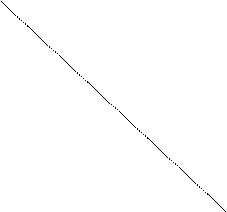
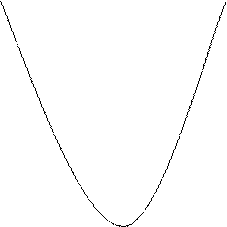
Пример 9. Сколько общих точек имеет парабола у=х2 и прямая х+у+m=0 (в зависимости от m)?
![]()
 Решение. Уравнение х+у+m=0
при разных m определяет различные прямые. При m=0 –
это биссектриса II и IV координатных углов, при m
Решение. Уравнение х+у+m=0
при разных m определяет различные прямые. При m=0 –
это биссектриса II и IV координатных углов, при m![]() 0 будут прямые, предельные этой биссектрисе.
0 будут прямые, предельные этой биссектрисе. 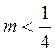 у
у
Наглядно легко себе представить, что при некторых значениях m
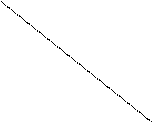 прямая пересекает параболу, при
прямая пересекает параболу, при 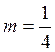
одном значении – касается, а при
 других значениях не имеет с ней
других значениях не имеет с ней 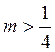
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.