Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 2

Длительное время разделение математики на «элементарную» и «высшую» соответствовало различию между школьной и вузовской математикой. В последние же десятилетия в школу проникли начальные разделы аналитической геометрии и математического анализа: уравнение прямых и плоскостей, производные, интегралы. Учитель математики, разумеется, должен изучить математику в значительно большем объеме, он должен видеть школьный курс, так сказать, с высшей точки зрения. Он не имеет права ограничивать свою роль изложением учебника «от» и «до», в этом случае он очень скоро стал бы неинтересен своим ученикам. Чтобы хорошо учить математике, учителю нужна фундаментальная математическая подготовка. Такой учитель сможет активно участвовать в совершенствовании математического образования в стране, он сможет осваивать и даже создавать новые приемы и методы преподавания, для него не будет проблемной переход к новым программам и учебникам.

Предлагаемый курса лекций адресован студентам педагогических институтов. От других аналогичных курсов он отличается тем, что при его построении принималось во внимание то печальное обстоятельство, что не все студенты 1 курса обладают достаточными знаниями школьной математики.

Пособие состоит из 7 глав, объединенных в две части – аналитическую геометрию на плоскости (и прямой) и в пространстве. Применяется такая нумерация: § 2.4. – это § 4 из главы 2; рисунок 2.3 – это рисунок 3 из главы 2; (2.4.3) - это формула 3 из § 2.4.

Часть 1. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ. НА ПЛОСКОСТИ

ГЛАВА 1. МЕТОД КООРДИНАТ НА ПРЯМОЙ И ПЛОСКОСТИ

§ 1.1. Координата точки на прямой

Пусть имеется прямая, на которой заданы точка О (начало координат) и точка Е. Направление луча ОЕ назовем положительным, противоположное - отрицательным; длину отрезка ОЕ  примем за 1 (рис. 1.1)

Положение произвольной точки М на прямой теперь можно  определить числом х, называемым координатой точки М. Координата определяется так:

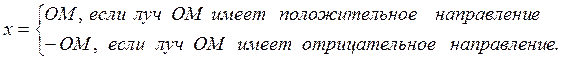
Тот факт, что х – координата точки М, записывается следующим образом:

М(х); иногда удобно и такое обозначение: х_м. Очевидно, О(0), Е(1).

Рассмотрим решение некоторых задач в координатах.

Задача 1. найти расстояние между точками А(х₁) и В(х₂).

Решение: состоит из нескольких частей в зависимости от расположения точек А и В относительно начала координат, то есть от знаков х₁ и х₂. Ввиду равноправия точек А и В нет надобности различать, например, случаи х₂>х₁>0 и х₁>х₂>0.

Поэтому для полного решения задачи достаточно рассмотреть лишь следующие варианты:

а) х₂>х₁=0                      в) х₂>х₁>0                      д) х₂<0<x₁

б) х₂<х₁=0                      г) х₂<х₁<0

поскольку рассуждения во всех случаях аналогичны, мы рассмотрим подробно лишь некоторые из них, представив читателю в остальных разобраться самостоятельно в) Если х₂>х₁>0 (рис. 1.2.), то х₁=ОА, х₂=ОВ и АВ=ОВ-ОА=х₂-х₁=|x₂-x₁|.

д) Если х₂<0<x₁ (рис. 1.3.), то х₁=ОА, х₂=-ОВ и АВ=ОА+ОВ=х₁-х₂=|x₂-x₁|.

Во всех случаях получается одна и та же формула расстояния между двумя точками:                      

AB=|x₂-x₁|                                           (1.1.1)

Примечание. Легко видеть, что знак разности x₂-x₁ показывает направление луча АВ: если х₂-х₁>0, то луч имеет положительное направление, если х₂-х₁<0 – отрицательное.

Определение. Пусть А – начало, В – конец отрезка и М – внутренняя точка отрезка АВ. Тогда отношением, в котором точка М делит отрезок АВ называется число .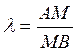

Задача 2. Найти координату точки М, делящей отрезок АВ в отношении λ, если А(х₁), В(х₂).

Решение. По формуле (1.1.1)           AМ=|x-x₁| и  МB=|x₂-x|, где х – координата точки М. Поэтому .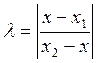

Но так как точка М находится между А и В, то  либо х₁<х<х₂ (как на рис. 1.4), либо х₂<х<х₁. В обоих случаях разности х-х₁ и х₂-х₁ одного знака и потому

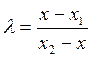
Решая это уравнение относительно х, получаем формулу деления отрезка в данном отношении:

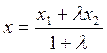                                         (1.1.2)