Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 17

2). Пары (2, 0) и (3, 0) пропорциональны, так как равенства 2=λ·3, 0=λ·0 имеют место при 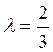. К тому же выводу придем, применяя условие (2.5.2): между дробями  и  можно поставить знак равенства, так как вторая равна любому числу, в частности, и числу .

Имея в виду сделанные разъяснения, можем считать условия (2.5.1) и (2.5.2) эквивалентными.

Теорема 1. (координатный признак коллинеарности векторов). Два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны.

Символическая запись:

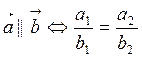                                   (2.5.3)

где .

Доказательство. Полагаем, что хоть один их двух данных векторов ненулевой, например, , так как в случае, когда оба вектора ненулевые, теорема тривиальна. Имеем на основании бескоординатного признака коллинеарности (знак эквивалентности 1) и теоремы 2 из § 2.4. (знак эквивалентности 2):

.

Мы пришли к условию (2.5.2). Теорема доказана.

Теорема 2. Для того, чтобы точки А(х₁, у₁), В(х₂, у₂), С(х₃, у₃) были коллинеарны (то есть лежали на одной прямой), необходимо и достаточно, чтобы выполнялось условие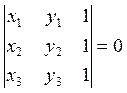

Это условие уже встречалось под номером (1.2.6), но вывод его в § 1.2. опирался на формулу площади треугольника, полное доказательство которой не было дано.

Доказательство. Точки А, В, С коллинеарны тогда и только тогда, когда  (рис. 2.16). Так как , то по признаку коллинеарности будет точки А, В, С коллинеарны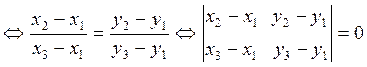

Непосредственным подсчетом можно убедится, что полученный определитель второго порядка равен определителю третьего порядка из условия теоремы. Однако, если читателю уже известны свойства определителей, то равенство двух определителей можно доказать и проще:

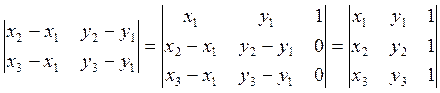
В § 1.1 и затем в § 1.2. рассматривалось отношение, в котором точка делит отрезок, причем делящая точка бралась внутри отрезка. Векторы позволяют не только упростить вывод формул (1.2.3) деления отрезка в данном отношении, но и обобщить само это понятие, «разрешив» делящей точке быть и вне отрезка.

Определение. Пусть А – начало, В – конец отрезка и М – точка прямой АВ. Тогда отношением, в котором точка М делит отрезок АВ называется число

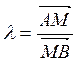
В этом определении использовано понятие отношения коллинеарных векторов, введенное в § 2.3.

По определению имеем:

            (рис. 2.17)

 не существует.

Подробнее. Если делящая точка М движется от А к В, то λ принимает все значения из промежутка . Когда точка М, «перепрыгнув» через В, будет удалятся в бесконечность, то λ будет принимать значения из промежутка . Если же точка М движется от А в бесконечность в противоположном направлении, то λ будет в промежутке . Таким образом, отношение в котором точка делит отрезок, может быть любым действительным числом, кроме -1.

Задача. Найти координаты точки М, делящей отрезок АВ в отношении λ, если А(х₁, у₁). В(х₂, у₂).

Решение. Пусть М(х, у). Тогда  и

.

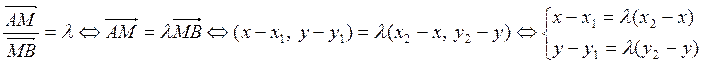Решая полученную систему относительно х и у, снова получаем формулы (1.2.3). Но теперь границы их применения шире, ибо мы исходили из более общего понятия деления отрезка в данном отношении.

§ 2.6. Проекция вектора на ось

Как и школьном курсе, под осью мы понимаем прямую, на которой установлена система координат.

Определение. Пусть А₁ и В₁ – ортогональные проекции концов вектора  на ось . Проекцией вектора  на ось  называется длина отрезка А₁В₁, взятая со знаком «+» или «-» в зависимости от направления вектора  (рис. 2.18).

Обозначение: . Согласно определению

                                        =      А₁В₁, если                        (2.6.1)

-А₁В₁, если

В

 

   А                                                                 А                 В                      М

С

Рис. 2.16                                                      Рис. 2.17

Аналогично можно рассматривать проекцию вектора на вектор. Проекция вектора может быть любым действительным числом – положительным, отрицательным или нулем.