Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 3

Ее частным случаем при λ=1 является формула деления отрезка пополам:

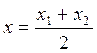                                           (1.1.3)

Имеющая такую словесную формулировку: координата середины отрезка равна полусумме координат его концов.

О(0)      Е(1)         М(х)                                     О                А      В

Рис. 1.1                                                           Рис. 1.2

В        О              А                                            А                       М              В

Рис. 1.3                                                           Рис. 1.4

§ 1.2. Прямоугольные декартовы координаты на плоскости

Пусть через точку О (начало координат) происходят две взаимно перпендикулярные прямые (оси координат): ОХ – ось абсцисса и ОУ – ось ординат. На осях координат заданы равные отрезки ОЕ и ОЕ₂, принимаемые за единичные. Теперь каждая точка М плоскости может быть задана упорядоченной парой чисел, называемых координатами, а по отдельности – абсциссой и ординатой. Абсциссой х точки М называется координата ее проекции М₁ на ось ОХ в той системе координат, которая устанавливается на прямой ОХ точками О и Е₁; ординатой – координата проекции М₂ на ось ОУ (рис. 1.5)

Обычные обозначения: М(х, у) или х_м, у_м. В этих обозначениях О(0, 0), Е₁(1, 0), Е₂(0, 1).

Координатные оси делят плоскость на 4 области, называемые I, II, III и IV координатными углами, как показано на рис. 1.6.

Рассмотрим решение некоторых задач в прямоугольных декартовых координатах.

Задача 1. Найти длину отрезка, если известны координаты его концов: А(х₁, у₁), В(х₂, у₂).

Решение. Предположим сначала, что отрезок не параллелен координатным осям (рис. 1.7) Обозначим через А₁ и В₁ проекции его концов на ось абсцисс, а через А₂ и В₂ – проекции на ось ординат. По формуле (1.1.1) будет .

Рассмотрим прямоугольный треугольник АВК, где К – точка пересечения прямых АА₂ и ВВ₁ (можно было взять за К и точку пересечения прямых АА₁ и ВВ₂). По катетам этого треугольника АК=А₁В₁ и ВК=А₂В₂ с помощью теоремы Пифагора находим гипотенузу: .

В окончательном виде формула расстояния между двумя точками записывается так:

                            (1.2.1)

Эта формула верна и тогда, когда отрезок АВ параллелен одной из осей. Например, если АВ || ох, то у₁=у₂ и по формуле (1.2.1) получаем , что соответствует формуле (1.1.1)

Отметим важный частный случай последней формулы – расстояние от начала координата до точки М(х, у):

                                    (1.2.2)

      у                                                                                 у

                                     М

    М₂                                                                      II                 I

Е₂                                                            x<0    y>0              x>0    y>0

                                                                                      О                                                  х

                                                 х                  x<0    y<0              x>0    y<0             

О                    Е₁         М₁                                          III                IV

Рис. 1.5                                                        Рис. 1.6

 

      у                                                                    у                                        В

     В₂                                                   В                                                                       

М

               А                          К                                           А

    А₂    

     

       О                А₁                   В₁     х                              О     А₁      М₁               В₁      х

Рис. 1.7                                                        Рис. 1.8