Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 8

                          (1.5.2)

Второе и третье неравенства (1.5.1), которые запишем несколько иначе:

a > b - c, a > c - b, равносильны одному неравенству . Поэтому система трех неравенств (1.5.1) равносильна двойному неравенству (1.5.2).

§ 1.6. Геометрический смысл неравенств между координатами

Мы будем рассматривать множество всех точек, координаты которых удовлетворяют некоторому неравенству. Начнем с примеров.

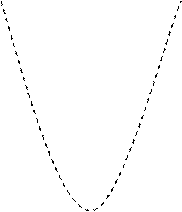
Пример 1. Неравенству y>x² удовлетворяют координаты всех точек, расположенных выше параболы y=x^2.. В самом деле, пусть точка М(х, у) расположена выше параболы (рис. 1.17). М₁ – ее проекция на ось абсцисс, а М₀(х, у₀) – точка пересечения отрезка ММ₁ с параболой; абсциссы точек М и М₀ одинаковы. Так как y>у₀ и y₀=x², то y>x².

Итак координаты произвольной точки М, расположенной выше параболы, удовлетворяют данному неравенству. Напротив, координаты точек параболы и координаты точек, лежащих ниже параболы, неравенству не удовлетворяют. Значит, данной неравенство определяет область выше параболы.

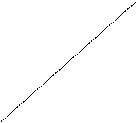
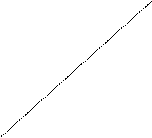
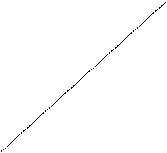
          Пример 2. рассмотрим неравенство . Ему удовлетворяют координаты всех точек, расположенных на окружности х² + у² =4 и во внешней области, но не удовлетворяют координаты точек, лежащих внутри круга (рис. 1.18). В самом деле, для любой внешней или лежащей на окружности точки М(х, у) имеем ОМ  2, то есть .

                    у                                                                          у

 

                              М                                                        М

·

                                                                                                       

                                   М₀                                                                    О                        х

 

                    О         М₁               х                                                        

 

Рис. 1.17                                                      Рис. 1.18

Пусть на плоскости имеется некоторая линия . Мы говорим, что эта линия разбивает множество не принадлежащих ей точек плоскости на части, называемое областями, если эти части обладают следующими двумя свойствами:

а) Две точки одной области можно соединить непрерывной линией^х, не пересекающей ;

б) Любая непрерывная линия, соединяющая две точки разных областей, пересекает .

Данная линия или ее части являются границами областей.

Например, прямая делит плоскость на две полуплоскости, границей которых она является; окружность разбивает плоскость на две области - внутреннюю и внешнюю; цифра «8» и буква «Ф» разбивают плоскость на три области каждая, а цифра «7» и буква «С» не производят разбиения плоскости или, можно сказать, «разбивают» плоскость на одну область.

Теорема 1. Пусть кривая , где  - непрерывная по обоим аргументам функция^хх, разбивает множество не принадлежащих ей точек плоскости на области. Если точки А и В принадлежат одной области, то значения функции в этих точках имеют один и тот же знак.

Под значением функции  в точке  мы подразумеваем число , которое принято обозначать также F(P). Отметим, что если F(P)=0, то точка Р находится на границе.

Нам требуется доказать, что F(A) и F(B) одного знака.

Доказательство. На рис. 1.19 область, в которой находятся точки А и В, обозначена α. Соединим данные точки кривой, целиком находящейся в области α. При движении точки М по этой кривой от точки А к точке В значение функции F(M) меняется непрерывно, причем оно не обращается в о, так как равенство F(М)=0 означало бы, что дуга АВ пересекает границу области. А это значит, что во всех точках дуги АВ функция имеет один и тот же знак.

Теорема доказана. Из нее следует, что функция  имеет один и тот же знак во всех точках области α.