Аналитическая геометрия. Методическое пособие для студентов физико-математического факультета, страница 7

(х² + 2х + 1) - 1 + (у² - 4у + 4) - 4+8 = 0

(х + 1)² + (у - 2)² = -3

В правой части - отрицательное число. Поэтому данное уравнение не есть уравнение окружности.

2) Приведение второго уравнения к виду (1.4.1) осуществляется таким же способом, только требуется предварительно разделить его на 3:

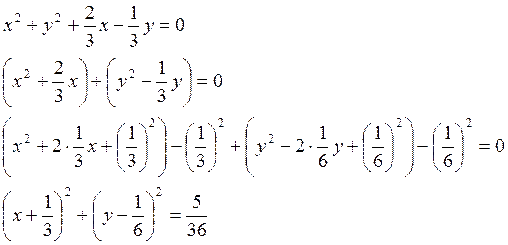
Данное уравнение есть уравнение окружности с центром в точке 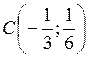 и радиусом 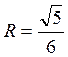. Отметим, что поскольку координаты точки О(0, 0) удовлетворяют уравнению окружности, она проходит через начало координат.

В заключение выведем параметрические уравнения окружности радиуса R с центром С(а, b).

Пусть М(х, у) – текущая точка окружности (рис. 1.15). Ее положение на окружности можно задать углом , где СН – луч, имеющий то же направление, что и ось ОХ. Этот угол мы и примем за параметр.

Обозначим через С₁ и М₁ проекции точек С и М на ось абсцисс. Рис. 1.15 сделан в предложении а,b>0, 0<t<. В этом случае а=ОС₁, С₁М=Rcost и х=ОС₁+С₁М₁=а+Rcost. Это соотношение, как легко видеть, выполняется не только в отмеченном случае, но и при других значениях а, b, t. Например, если 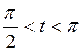, то С₁М₁=-R cost и поскольку х=ОС₁-С₁М₁, то приходим к той же формуле. Аналогично получаем у=b+Rsint. Итак, параметрические уравнения окружности таковы:

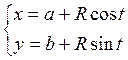                            (1.4.3)

§ 1.5. Существование треугольника с заданными сторонами

                                   у

                                                                           К

b                    с     

                                    О                     а                          А           х

Рис. 1.16                                                                                  

Из школьного курса известно. Что в треугольнике сумма двух любых сторон больше третьей. Это значит, что для того, чтобы из отрезков а, b, с можно было составить треугольник, необходимо выполнение следующих неравенств:

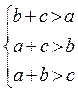                          (1.5.1)

Выясним, достаточны ли эти условия. Решение этого вопроса – пример применения уравнения окружности.

Теорема. Для того, чтобы три отрезка могли служить сторонами треугольника, необходимо и достаточно, чтобы сумма любых двух из них была больше третьего.

Условие теоремы можно представить в следующем виде:

Существует треугольник cо сторонами а, b, c              Д <=> П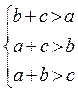     

Доказательство: как отмечено выше, необходимость условия (на схеме обозначено буквой «Н») известна из школьного курса. Докажем достаточность (на схеме буква «Д»): даны неравенства (1.5.1), требуется доказать, что треугольник с данными сторонами существует.

Из концов отрезка ОА=а как из центров опишем окружности радиусов b и с соответственно (рис. 1.16). Докажем, что при выполнении неравенств (1.5.1) окружности пересекаются. Если К – точка пересечения, то треугольник ОАК искомый.

Выберем систему координат: О – начало; ОА – положительный луч оси ОХ. Уравнение окружностей образуют систему

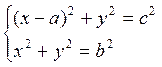
Чтобы треугольник со сторонами а, b, с существовал, необходимо и достаточно, чтобы система имела два решения, соответствующих двум точкам пересечения, симметричным относительно оси абсцисс.

Из первого уравнения вычтем второе. Получим систему

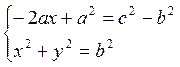
Равносильную исходной. Из первого уравнения 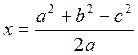. Это выражение подставим во второе уравнение и вычислим у²: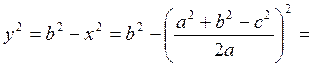

=

.

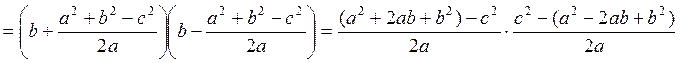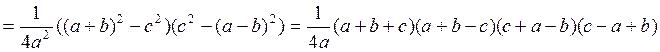Отсюда видно, что в силу неравенства (1.5.1) у² имеет положительное значение. Следовательно, исходная система имеет два решения, окружности пересекаются и треугольник с данными сторонами существует.

Теорема доказана.

Следствие 1. Для существования треугольника со сторонами а, b, с необходимо и достаточно, чтобы больший из этих отрезков был меньше суммы двух других.

В самом деле, если , то второе и третье неравенства (1.5.1) выполняются тривиальным образом, а оставшееся первое как раз и соответствует формулировке следствия.

Следствие 2. Для существования треугольника со сторонами а, b, с необходимо и достаточно, чтобы какой-нибудь из этих отрезков был меньше суммы, но больше абсолютной величины разности двух других, например