Навигационные системы. Часть 1. Гироскопические приборы и устройства навигационных систем: Учебное пособие, страница 9

представив кинетический момент  в виде суммы его основной составляющей  и составляющей

.  

Из (3) следует

                                                                    (26)

Но, как было показано выше,

поэтому (26) можно представить в виде

 ,                                                               (27)

аналогичном (25) и отличающимся от этого равенства лишь тем, что инерционный момент представлен в виде суммы его преобладающей составляющей, отражающей специфику гироскопа - гироскопического момента - и "обычной" для вращающегося тела составляющей , обусловленной угловым ускорением, вид которой легко усматривается из уравнений (8) движения гироскопа (первые слагаемые в левых частях уравнений, но взятые с противоположным знаком). Если в (27) последней составляющей пренебречь, то получится уравнение

                                                                             (28)

записав которое в проекциях на оси x₁  и y₁ резалевой системы  координат, мы получим уже рассматривавшиеся выше укороченные,        или прецессионные уравнения движения гироскопа. Уравнение        (28), как правило, и используется при выводе уравнений движения гироскопических устройств в инженерной практике.

             1.5. Уравнения движения гироскопа в кардановом подвесе

Приведенные выше результаты необходимо уточнить, для чего, в частности, необходимо учесть наличие подвеса гироскопа. Очевидно, что без подвеса практическое    использоёвание гироскопа невозможно, а подвес участвует в движении гироскопа. В качестве подвеса на практике используют двух-, трехстепенной и трехстепенной с дополнительной рамкой кардановы подвесы в зависимости от назначения прибора, которым определяется требуемое число степеней свободы гироскопа. Одна из степеней свободы, связанная с собственным вращением, реализуется конструктивно в гиромоторе (рис.2), размещаемом обычно в кожухе, играющем роль внутренней рамки подвеса. Двухстепенной подвес (рис.8) обеспечивает возможность разворота оси гироскопа относительно лишь одного из направлений, перпендикулярных его оси собственного вращения - по углу  b. Такие гироскопы называют двухстепенными.

Трехстепенной подвес  (рис.9) обеспечивает возможность разворота оси гироскопа относительно двух направлений - по углам a и   b (трехстепенной  гироскоп). Однако,  если  в   этой схеме  гироскоп развернется на угол b, равный 90^o (или кратный ему),  то ось собственного вращения гироскопа совместится с наружной осью  подвеса и при этом гироскоп  потеряет возможность вращаться вокруг вертикальной оси (эффект "сложения рамок подвеса"). Поэтому, если гироскоп предназначен для использования в условиях его возможного произвольного разворота, он оснащается трехстепенным подвесом с дополнительной рамкой. Рис.10 иллюстрирует один из возможных вариантов подобного подвеса.

Рассмотрим теперь вопрос о том, как изменятся уравнения движения гироскопа (8) с учетом наличия карданова подвеса. Для конкретности будем полагать, что гироскоп оснащен трехстепенным подвесом, изображенным на рис.9 (отсчет углов на этом рисунке согласован с рис.1). При этом учтем также тот факт, что моменты могут быть приложены к гироскопу только путем создания моментов по осям подвеса a и b. При этом связь между моментами М_a и М_b,  приложенными по осям подвеса, и моментами М_x1 и М_y1, создаваемыми при этом по резалевым осям  x₁  и y₁, имеет вид

.

Для получения искомых уравнений следует повторить выполненные ранее выкладки, дополнительно учтя вектор кинетического момента элементов карданова подвеса. В результате будем иметь следующие уравнения, аналогичные (8):

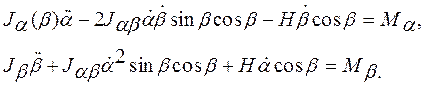                                                   (29)

Здесь

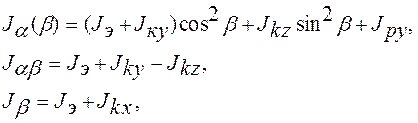
J_э - экваториальный момент инерции гироскопа, J_kx, J_ky, J_kz - моменты инерции кожуха гироскопа относительно резалевых осей  x₁, y₁, z₁ соответственно (см. рис.8), J_py - момент инерции рамки (Р на рис.9) относительно оси вращения  по углу  a.