Навигационные системы. Часть 1. Гироскопические приборы и устройства навигационных систем: Учебное пособие, страница 3

Особо следует упомянуть в этой связи развиваемое в последнее время направление создания миниатюрных измерителей   параметров движения – микромеханических гироскопов и акселерометров. Они пока не удовлетворяют требованиям точной навигации и потому в данных лекциях не рассматриваются. С указанным новым направлением можно познакомиться, например, по обзорной статье М.И.Евстифеева (см. список литературы), а также по ряду статьей, опубликованных в журнале «Гироскопия и навигация».

                1. Основные сведения из теории гироскопа

1.1. Движение абсолютно твердого тела вокруг неподвижной точки

Для описания движения тела вокруг неподвижной точки О  введем две ортогональные правые системы координат: систему координат Оxyz, связанную с телом и ориентированную относительно него пока произвольным образом, и неподвижную, инерциальную систему координат Oxhz. Тогда ориентация тела в инерциальном пространстве будет определяться взаимной ориентацией введенных систем координат. Она же характеризуется тремя эйлеровыми углами  a, b и j , вводимыми, например, так, как показано на рис.1. На этом рисунке изображены также векторные составляющие    угловой скорости разворота тела  на упомянутые углы. Из астрономии в гироскопию перешли названия вращательных движений по углам a, b, j:  соответственно прецессия, нутация и ротация (или собственное вращение). Однако, правильнее связывать указанные  составляющие вращательного движения тела с причинами, их вызывающими, о чем будет сказано ниже.

Используя рис.1 и обозначая индексом "о" орт соответствующий оси можно записать связь векторов    с их величинами    

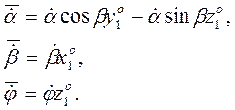                                                      (1)

Сумма векторов    есть, очевидно, угловая скорость тела , т.е.

Проектируя обе части этого равенства на оси связанной системы координат, используя при этом принятые в теоретической механике обозначения для проекций вектора

, с учетом (1) получим

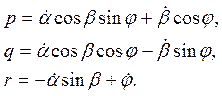                                                (2)

Это - кинематические уравнения Эйлера для вращательного движения тела вокруг неподвижной точки. Они связывают составляющие угловой скорости тела с углами, характеризующими ориентацию тела.

Уравнения, связывающие составляющие угловой скорости с   действующими на тело моментами называются динамическими уравнениями. Впервые они были получены также Эйлером. Выводятся эти уравнения на базе фундаментальной теоремы теоретической механики об изменении момента количества движения (кинетического момента) тела. Согласно этой теореме

,                                                                                    (3)

где   - суммарный момент, действующий на тело. Если теперь, воспользовавшись произвольностью выбора ориентации связанной системы координат, направить оси x, y, z по главным осям инерции тела, то выражение для  будет иметь достаточно простой вид

                                                         (4)

где   J_x, J_y, J_z  - моменты инерции тела относительно осей   x, y и z соответственно. Подставляя (4) в (3) и проектируя обе части векторного уравнения на оси связанной системы координат,  получим требуемые динамические уравнения

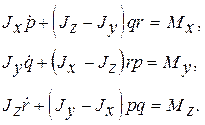                                                              (5)

Полную систему уравнений вращательного движения твердого тела вокруг неподвижной точки составляют кинематические уравнения  (2), динамические уравнения (5) и соотношения для определения  составляющих момента, имеющие в общем случае вид

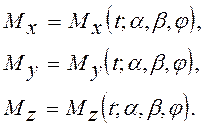                                                              (6)

Для получения решения этой системы, описывающего вращение тела, необходимо задать начальные условия: значения на начальный момент времени углов a, b, j и составляющих угловой скорости  p, q, r.

Даже при условии, что на тело действует момент, обусловленный только силой тяжести, приведенная система уравнений допускает получение решения в элементарных функциях лишь в отдельных случаях (случаи Эйлера-Пуансо, Лагранжа-Пуассона и Ковалевской).