Как уже упоминалось, под гироскопом понимается осесимметричное тело, вращающееся вокруг оси симметрии с достаточно большой скоростью. Будем полагать, что с осью симметрии тела совпадает ось z. Тогда моменты инерции Jx и Jy одинаковы; обозначим их величину Jэ. Эта величина называется экваториальным моментом инерции. Величина же Jz называется осевым моментом инерции.
Условие, что тело вращается вокруг оси симметрии с
"достаточно большой" угловой скоростью означает, что величинами
и 
можно пренебречь по сравнению с 
. С учетом этого, как вытекает из (2) и
(4),
т.е. кинетический момент гироскопа можно считать направленным по оси его собственного вращения (называемой далее для краткости осью гироскопа), а его величину считать равной произведению осевого момента инерции и скорости собственного вращения. Эту величину общепринято обозначать буквой H:
Она является основной характеристикой гироскопа: чем больше H, тем в большей степени проявляются гироскопические свойства вращающегося ротора.
С учетом указанных выше отличительных особенностей гироскопа динамические уравнения (5) упрощаются. Действительно, принимая во внимание, что
эти уравнения можно записать в виде:
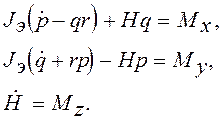(7)
Вместе с соотношениями (2) и (6) они описывают движение гироскопа.
Полученную систему уравнений целесообразно подвергнуть дальнейшему упрощению. В частности, желательно исключить из нее переменную j, поведение которой, в отличие от углов a и b, при анализе движения гироскопа интереса не представляет. С использованием приведенных выше формул это можно сделать следующим образом. Значения p, q, r из (2) подставим в первые две формулы (7), после чего полученные два соотношения сложим сначала с множителями cosj и - sinj, а затем с множителями sinj и cosj. В результате получим
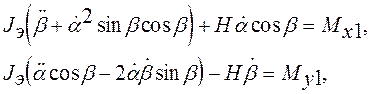(8)
где
- составляющие действующего на гироскоп
момента по осям x1 и y1
соответственно. Уравнения (8)
совместно с третьим уравнением (7) и соотношениями для определения
моментов Mx1, My1, Mz составляют
полную систему уравнений для определения углов a и b, характеризующих текущую ориентацию оси гироскопа
или, что то же, системы координат, показанной на рис.1 - Ox1y1z1.
Указанная система координат связана с гироскопом, но не участвует в его собственном вращении. В честь ученого Резаля, внесшего существенный вклад в теорию гироскопа, она называется резалевой системой координат. Нетрудно уяснить, что уравнения (8) вместе с третьим уравнением (7) представляют собой те же динамические уравнения, но в проекциях на оси резалевой системы координат.
Теперь заметим, что в приборах, использующих гироскоп, поддерживается постоянная скорость его собственного вращения. Поэтому в (8) величину H можно считать константой. С учетом этого обстоятельства система уравнений (8) при заданных Mx1 и My1 полностью описывает движение гироскопа, если под этим движением понимать вращательное движение оси гироскопа.
Отметим некоторые особенности уравнений (8). Если бы
на гироскоп действовал только момент Mx1 и гироскоп не был разогнан (
),
то его движение описывалось бы простым уравнением для тела, вращающегося вокруг
оси x1:
(9)
интегрированием которого определяется угол поворота b гироскопа вокруг x1. Вследствие же собственного вращения гироскопа, даже при действии только момента Mx1, в левой части уравнения (9), как видно из первого уравнения (8), появляются дополнительные члены. При этом второй из этих членов, т.е. Hcosb, при большой величине H значительно превосходит остальные члены левой части, т.е. с достаточной точностью можно записать
(10)
откуда видно, что для разогнанного гироскопа действие момента по оси x1 приводит в большей мере к изменению угла a, т.е. к вращению гироскопа не вокруг оси x1, а вокруг оси h, перпендикулярной x1. В этом - одна из особенностей гироскопа.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.