Рассмотрим принцип работы гиротрона.
Для этого выделим элемент Dm вибрирующего стержня
(рис.36) и рассмотрим его движение. Вследствие вибрации он имеет линейную
скорость 
в плоскости вибрации; величину этой скорости
можно считать изменяющейся по гармоническому закону 
|
|
где А - амплитуда колебаний, зависящая от места расположения элемента Dm в стержне, w - круговая частота собственных колебаний вибратора. При вращении элемента вместе со стержнем вокруг оси x с угловой скоростью ux возникает кориолисово ускорение
Но наличие у элемента этого ускорения означает, что с его стороны на стержень действует сила D¦, равная по величине
Эти элементарные силы, направление которых на протяжении полупериода колебаний одинаково для всех элементов одного стержня (рис.37), создают моменты
, где
2r - расстояние между стержнями. Суммирование элементарных моментов дает
результирующий момент
где k1 - умноженный на 4r интеграл по всей массе вибратора от величины Аw, т.е. константа.
|
|
Нетрудно видеть, что момент Мг имеет ту же природу, что и гироскопический момент, что оправдывает отнесение гиротрона к гироскопическим приборам.
Составим теперь уравнение движения вибратора вокруг оси x, обозначив a - угол скручивания торсиона, J - момент инерции вибратора относительно оси x, h - коэффициент вязкого трения, С - коэффициент упругости торсиона:
(57)
Это, как видно, уравнение колебательного звена (заметим, что h - малая величина) с гармоническим возмущением. После завершения переходного процесса, описываемого решением уравнения (57) при нулевой правой части и заданных начальных условиях, поведение a будет описываться частным решением уравнения (57). Как известно, для линейного дифференциального уравнения с гармонической правой частью частное решение также является гармонической функцией той же частоты (за исключением случая совпадения частоты возмущающей силы с корнем характеристического полинома дифференциального уравнения).
При этом амплитуда гармоники
(58)
где
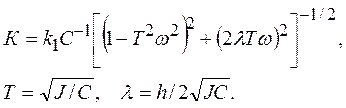(59)
Таким образом, выходной сигнал гиротрона представляет собой гармонический сигнал с частотой, равной собственной частоте вибратора, и с амплитудой, пропорциональной (с известным коэффициентом пропорциональности) измеряемой угловой скорости ux. Для того, чтобы повысить добротность прибора, целесообразно его параметры подобрать так, чтобы максимизировать К. Как следует из (59), с учетом малости l максимум достигается при Тw =1, т.е. при совпадении частоты собственных колебаний вибратора с собственной частотой его колебаний вокруг оси x . При этом
К=k1/2lC.
Это обстоятельство используется на практике.
Гиротрон - достаточно простой и удобный в эксплуатации прибор. Однако, он представляет определенные сложности в производстве (в частности, требует высокой точности изготовления деталей, тщательной балансировки), требует применения высокочувствительного датчика угла и (для обеспечения приемлемой точности) поддержания стабильной рабочей температуры.
|
|
Гироскопический интегратор угловой скорости (ГИУС) предназначен для измерения интеграла от
проекции абсолютной угловой скорости объекта на ось чувствительности прибора.
Схема прибора изображена на рис.38. ГИУС включает двухстепенной астатический гироскоп
1, датчик угла 2 и демпфер 3. Как видно, схема ГИУС отличается от схемы
ГТ только отсутствием пружины. Как и в ГТ, выходным сигналом ГИУС является
угол b поворота гироскопа вокруг оси подвеса x. Он снимается с датчика угла 2. Ось чувствительности прибора - ось h, которая есть перпендикуляр к оси x и вектору 
при b= 0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
