Навигационные системы. Часть 1. Гироскопические приборы и устройства навигационных систем: Учебное пособие, страница 6

Поскольку  есть скорость конца вектора кинетического момента, то равенство (3) применительно к гироскопу можно трактовать следующим образом: скорость конца вектора кинетического момента гироскопа равна моменту, приложенному к гироскопу (теорема Резаля).

Итак, приложение к гироскопу момента вызывает изменение его ориентации, т.е. к вращению оси гироскопа. Это вращение под действием момента называют прецессией гироскопа. Найдем скорость прецессии, обозначив ее . Очевидно, что вектор  ортогонален оси гироскопа (поскольку угловая скорость, имеющая направление оси, к изменению ориентации этой оси не приводит).

Далее,  ортогонален , а модули этих двух векторов равны (это следует из самого определения понятия угловой скорости). Из сказанного вытекает следующее выражение для

 .                                                                             (15)

Далее, поскольку с достаточной точностью

,                                                                                   (16)

то из (3) с учетом постоянства H получаем

и после подстановки в (15)

.                                                                       (17)

Из изложенного вытекает второе основное свойство гироскопа: при действии на гироскоп момента он прецессирует с угловой скоростью, определяемой равенством (17).

Нетрудно видеть, что прецессия происходит в плоскости, параллельной вектору момента и оси гироскопа, при этом гироскоп стремится совместить свою ось с направлением момента по кратчайшему пути ,как  показано на рис.3.Изложенное еще раз поясняет отмеченную в п.1.2 особенность поведения гироскопа. Следует отметить, как и ранее, что описанное свойство реализуется с тем большей точностью, чем больше Н. Строго же оно не реализуется по той причине, что использованное при его выводе равенство (16) -приближенное, хотя и достаточно точное, - в нем не учтены инерционные члены, содержащие J_э. Но при тех же условиях получены и уравнения (10), (11), которые, следовательно, отражают прецессионное движение, почему и называются прецессионными. Как уже отмечалось, при решении большинства прикладных задач оказывается вполне допустимым ограничиться рамками прецессионной теории.

Заметим, что в рамках этой теории гироскоп является безынерционным прибором: его прецессия возникает и исчезает одновременно с приложением и прекращением действия момента. При этом последний не совершает никакой работы, поскольку вызываемая им прецессия гироскопа происходит со скоростью, перпендикулярной этому моменту.

Возникает естественный вопрос: как изменятся сформулированные выше утверждения, если не пренебрегать инерционными членами? Иными словами, насколько корректно ограничиваться рамками прецессионной теории? Для ответа на этот вопрос рассмотрим представляющий самостоятельный интерес случай движения гироскопа, проанализированный Лагранжем и Пуассоном. Выводы,    которые будут сделаны по результатам этого рассмотрения, распространимы и на общий случай. В случае Лагранжа-Пуассона момент, прикладываемый к гироскопу, создается силой тяжести , т.к. полагается, что центр масс гироскопа смещен относительно центра вращения в направлении оси гироскопа на величину (рис.4). Для упрощения рассмотрения будем полагать, что углы a  и b малы, и в этом предположении запишем уравнения движения гироскопа (8), удерживая только члены первого порядка  малости:

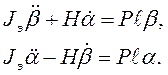
Решение этой линейной системы уравнений может быть получено достаточно просто и представимо в виде

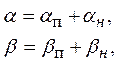                                                    (18)

где

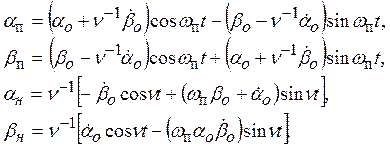(19)

Здесь    - начальные условия,

n=H/J_э,  w_п = Р/H.               

Из (18) и (19) следует, что движение гироскопа представляет собой сумму двух гармонических движений, одно из которых совершается с малой круговой частотой  w_п (ее величина обратно пропорциональна большой величине Н), а другое - с высокой частотой n (величина которой прямо пропорциональна Н). Результирующее движение иллюстрируется рис.5.