Навигационные системы. Часть 1. Гироскопические приборы и устройства навигационных систем: Учебное пособие, страница 27

Для съема   информации  в  приборе  имеются  два  датчика   перемещений ДУ_x и ДУ_h   индукционного типа, расположенные в двух взаимно-перпендикулярных плоскостях, проходящих   через ось вращения    z. Очевидно, можно считать, что датчики измеряют углы a_x и  a_h поворота ротора вокруг осей x (ДУ_h) и h (ДУ_x), перпендикулярных оси  z  и лежащих в упомянутых выше плоскостях.

Прибор выдает информацию о составляющих абсолютной  угловой скорости объекта по осям x и h.

Принцип работы ВРГ не отличается от принципа  работы  уже рассмотренных приборов.  При наличии скорости объекта,  например, вокруг оси x, гироскоп прецессирует вокруг оси h до  тех пор, пока  гироскопический  момент вследствие вынужденной прецессии не уравновесится упругим моментом стяжек. При этом угол поворота гироскопа, фиксируемый датчиком ДУ_x, в линейном  приближении пропорционален скорости объекта u_x.

Более строго этот результат можно получить,  анализируя уравнения   движения  ВРГ. Запишем эти уравнения, ограничиваясь  рамками прецессионной теории и  пренебрегая  массами стяжек и кольца. Предварительно установим  следующий  факт: момент   упругости   стяжек  с одинаковым коэффициентом  упругости С каждая при отклонении  гироскопа  вокруг h  на  угол  a_h  имеет нулевую составляющую по оси x и составляющую

по  оси h,  которые не зависят  от положения ротора, т.е. угла j  (рис.34). Действительно,  при развороте  ротора на a_h  углы скручивания стяжек 1 составляют

a₁ = a_hcosj,     (53)

а создаваемый ими момент упругости в проекциях на оси  x и h

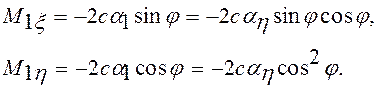
Углы скручивания стяжек 2

,                                                         (54)

а создаваемый ими момент упругости

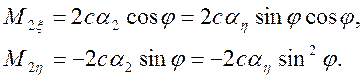
Суммарный момент упругости

что и  требовалось.  Отсюда  вытекает,  что независимо от угла собственного вращения j ротора момент упругости равен произведению 2С на величину отклонения ротора и направлен так,  что препятствует этому отклонению.  Очевидно,  то же имеет место и по отношению к моменту сил вязкого трения.

Запишем теперь уравнение моментов с учетом принятых ранее допущений и малости углов  a_x и  a_h. В проекции на ось h и x соответственно

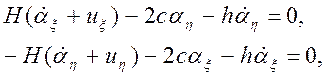
где   u_x, u_h - составляющие абсолютной угловой скорости объекта, h - коэффициент вязкого трения.  Из этих уравнений нетрудно получить уравнения для   a_x и a_h. Для    a_x  (учитывая, что h - малая величина)

                            (55)

где Т = Н/2С,   l = h/Н. Для a_h

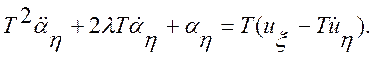                            (56)

(Заметим, что соотношения (55) и (56) менее трудоемко  получаются с использованием операционного исчисления).

Из полученных соотношений следует, что ВРГ является колебательным звеном  и после затухания переходного процесса и при отсутствии угловых ускорений объекта его выходные сигналы пропорциональны составляющим u_x и u_h  абсолютной угловой скорости объекта. Влияние на выходные сигналы углового ускорения можно рассматривать как ошибку, но более эффективно учитывать его аналитически при совместной отработке обоих сигналов  a_x и  a_h.

Заметим, что если угловая скорость  объекта,  а  следовательно  и  величины    a_x , a_h постоянны, то  углы  скручивания стяжек, как это следует,  в частности, из (53) и (54), изменяются с высокой частотой, равной скорости вращения ротора  . С этой частотой колеблется (вибрирует) кольцо.  Наличие вибрационной частоты и обусловило название гироскопа.

ВРГ, как видно,  прост по конструкции. Он имеет малые вес и габариты, но характеризуется недостаточно высокой точностью.

6.3. Гиротрон

Вибрационный   стержневой гироскоп, или гиротрон, представляет собой прибор,  изображенный на рис.35.  Он включает вибратор  1  типа камертона на  торсионе 2,  датчик угла 3 индукционного  типа  и  элементы    возбуждения и поддержания   колебаний   4.  Прибор  измеряет составляющую абсолютной  угловой скорости объекта по оси  x.

Принципиальное отличие гиротрона от  ранее  рассмотренных гироприборов состоит в том, что вращающегося ротора в нем нет, его заменяют вибрирующие стержни.