Навигационные системы. Часть 1. Гироскопические приборы и устройства навигационных систем: Учебное пособие, страница 5

Уравнение (10) и получаемое аналогичным образом из второго уравнения (8) уравнение

                                                                             (11)

называются укороченными уравнениями движения гироскопа, или уравнениями прецессионного движения (прецессионными уравнениями). Смысл второго названия будет раскрыт ниже. Укороченные уравнения являются, очевидно, приближенными, но вполне приемлемыми при решении большинства практических задач. Они тем более точны, чем больше H. Большая же величина H  обеспечивается соответствующей конструкцией гироскопа, при которой достигается наибольшее значение осевого момента инерции, и разгоном ротора до весьма больших угловых скоростей. В частности, вместо обычных двигателей в гироскопии используют двигатели, в которых вращающийся ротор располагается не внутри, а вне статора (рис.2), что дает существенный эффект в увеличении осевого момента инерции (так называемый обращенный подвес ротора). Что же касается угловой скорости вращения ротора, то она составляет величину в несколько десятков тысяч оборотов в минуту.

1.3. Основные свойства движения гироскопа

Рассмотрим сначала случай, когда на гироскоп не действуют никакие моменты, т.е. в (3)  (случай Эйлера-Пуансо). Такой гироскоп называют свободным. Чтобы гироскоп был свободным, в частности, должно выполняться условие совпадения его центра масс с центром О вращения, т.е. гироскоп должен быть астатическим. Для свободного гироскопа согласно (3)

т.е сохраняет свою величину и направление в инерциальном пространстве. Но поскольку, согласно предыдущему п.1.2, с достаточно высокой точностью

 где

то отсюда вытекает первое основное свойство гироскопа: ось свободного гироскопа сохраняет свою ориентацию в инерциальном  пространстве.

Строго говоря, это свойство реализуется в некотором приближении, но тем точнее, чем больше кинетический момент гироскопа.

Для практики важен ответ на вопрос: как изменится ориентация свободного гироскопа, если на него подействует какое-то кратковременное возмущение? Иными словами, устойчиво ли свободный гироскоп сохраняет свою ориентацию? Для ответа на этот вопрос обратимся к уравнениям (8), полагая, что ориентация инерциальной и резалевой систем координат выбрана так, что положению гироскопа до воздействия на него возмущения соответствовали углы    a(t)= 0,    b(t) = 0. Запишем уравнения (8) в отклонениях от упомянутого невозмущенного движения в линейном приближении, сохранив, для упрощения записи, за отклонениями углов обозначения a  и b:

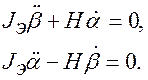                                                                          (12)

Результатом кратковременного воздействия на гироскоп возмущения является появление отклонений в углах a, b и в скоростях   - обозначим их  a_о, b_о,  - которые можно рассматривать как начальные условия для возмущенного движения гироскопа. Решение системы (12) может быть легко получено; при указанных выше начальных условиях оно имеет вид:

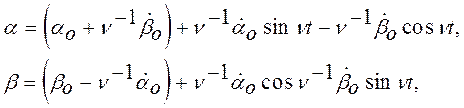                                       (13)

где

.                                                                      (14)

Нетрудно видеть, что соотношениям (13) соответствует такое движение гироскопа, при котором его ось описывает конус, направление оси которого задается углами

, а полураствор равен

.

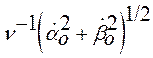Приведенные выкладки свидетельствуют о том, что в результате воздействия на гироскоп кратковременного возмущения он изменит свою ориентацию, но величина этого изменения ограничена и тем меньше, чем меньше возмущение и больше Н. Иными словами, свободный гироскопсохраняет свою ориентацию устойчиво, хотя и не асимптотически (т.е. его отклонения, вызванные воздействием возмущения, со временем не увеличиваются, но и не исчезают).

Пусть теперь гироскоп не является свободным и на него действует момент . Тогда согласно (3)

.