Навигационные системы. Часть 1. Гироскопические приборы и устройства навигационных систем: Учебное пособие, страница 30

 Динамически настраиваемый гироскоп (ДНГ) схематично изображен на рис.40. Он включает ротор 1,     восемь стяжек 2,     два кольца 3,4,      двигатель  Дв      и   датчики перемещений  ДУ_x   и ДУ_h. Как видно, подобно вибрационному  роторному гироскопу  (рис.33),  ДНГ - трехстепенной гироскоп с  упругим обращенным   подвесом.  На схеме рис.40,  в отличие от  рис.33, изображено  два кольца  и восемь ( а не четыре)  стяжки. Но это отличие не является    принципиальным; принципиальным же различием является то, что если в ВРГ кольцо играло второстепенную роль элемента крепления, то в ДНГ кольца обеспечивают требуемое функционирование прибора. А задачей ДНГ является измерение интегралов от составляющих  u_x и u_h абсолютной угловой  скорости  основания  по осям x  и  h  (в отличие от ВРГ, измеряющего сами  составляющие). Интегрирующий эффект достигается  настройкой  гироскопа,  заключающейся в соответствующем подборе скорости вращения j ротора, коэффициента упругости С стяжек, осевых J_о и экваториальных J_э моментов инерции колец. Благодаря этой настройке гироскоп, находясь в упругом подвесе,  ведет себя как  свободный гироскоп.

 Рассмотрим работу ДНГ.

 Для этого  составим  уравнения  движения  колец,  начав с  кольца  3 и пользуясь рис.41. На этом рисунке оси  x₃ и y₃  связаны  с кольцом 3. Это кольцо вращается вокруг оси со скоростью  и  может  разворачиваться относительно  основания только вокруг  оси  x₃. Угол этого разворота обозначим a_x.  Тогда проекции   относительной  угловой скорости   кольца   на  связанные с ним оси     x₃, y₃  и  z₃ можно записать соответственно в виде

(при этом считается, что угол   a_х мал).

 Полагая, что переносная скорость - скорость  основания  -  мала по сравнению с относительной скоростью кольца,  приведенные выражения можно принять  за  проекции  абсолютной  угловой скорости кольца. Запишем теперь уравнения движения кольца вокруг оси x₃, используя уравнения Эйлера (5)

.

Здесь   М_р-к3     - момент, с которым ротор действует на  кольцо  3  через соединяющие  их  стяжки.  Из этого соотношения вытекает,  что кольцо 3 прикладывает к ротору момент относительно оси   x₃,  равный

 Относительно же оси   y₃ кольцо 3 действует на ротор с моментом

 где  a_y - отклонение ротора вокруг  оси  y₃ кольца (последнее  удерживается от вращения вокруг   y₃ стяжками).

 Аналогичный анализ движения кольца 4 приводит к следующим  выражениям для  моментов,  с  которыми это кольцо действует на  ротор (по осям    x₄  и  y₄, связанным с кольцом 4)

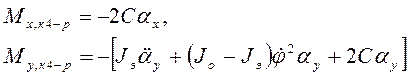
(при этом инерционные характеристики колец полагаются одинаковыми).

 Суммарные моменты, действующие на ротор со стороны колец,  равны

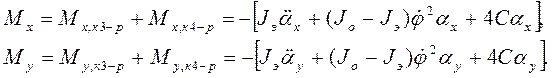
 Но как было выяснено при рассмотрении ВРГ (раздел 6.2) функции a_x   и    a_y   являются гармониками с круговой частотой  . Принимая

 для    M_x получим

 Этот момент обращается в нуль при условии

                                                       (61)

 Аналогично показывается,  что при выполнении условия (61)  в нуль обращается и момент   M_y.

 Выражение (61) есть условие динамической настройки гироскопа в упругом подвесе;  если оно выполняется,  то на ротор не  действуют моменты и он,  согласно первому основному  свойству,  сохраняет свою ориентацию в инерциальном пространстве неизменной.

 Записывая теперь  уравнение  моментов для ДНГ в проекциях  на оси       x  и  h (рис.40), получим при малых    a_x  и  a_h

откуда и вытекает, что определяемые с помощью датчиков ДУ_x  и ДУ_h    углы a_x   и  a_h  есть интегралы

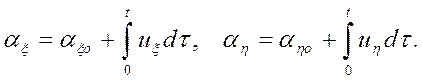
 Заметим, что вследствие ограничения на величины углов   a_x   и   a_h         (а оно вытекает из того,  что закон Гука  пропорциональности деформаций вызывающим  их силам справедлив в ограниченном диапазоне деформаций) ДНГ может использоваться,  как и ПИГ, в основном, в индикаторном режиме.