В проекциях на оси резалевой системы координат это равенство дает два скалярных соотношения
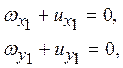
где
составляющие относительной скорости 
равны
а составляющие переносной скорости
(что вытекает из рис.11). Из полученных соотношений следуют искомые выражения для составляющих видимого ухода
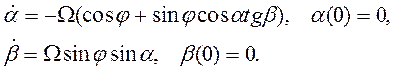
При
иной ориентации гироскопа относительно вертикали и стран света выражения для
и 
будут,
естественно, иными.
Из вида уравнений, описывающих движение гироскопа, видно, что он является достаточно сложным нелинейным объектом. В связи с этим при исследовании работы и при проектировании систем, включающих в свой состав гироскоп, возникает задача его представления линейной моделью, позволяющей применить эффективные методы анализа устойчивости и точности, развитые в теории линейных систем автоматического регулирования. Для получения линейной модели, как известно и как это уже делалось в разделе 1.3, нелинейные функции, входящие в уравнения, раскладываются в ряд в окрестности исследуемого опорного (невозмущенного) движения и сохраняются лишь первые, линейные члены этих разложений. Полученная линейная система и используется в качестве линейной модели, описывающей возмущенное движение в отклонениях от опорного.
Выпишем, в частности, уравнения возмущенного движения гироскопа в трехстепенном подвесе (рис.9), полагая, что невозмущенному (опорному) движению соответствуют значения a(t)=0, b(t)=0.
Из уравнений (29) получим
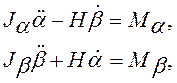(32)
где
Ja =Jэ+Jky+Jpy, Jb=Jэ+Jkx. На основании этих уравнений трехстепенной гироскоп
с позиций теории автоматического регулирования можно рассматривать как
линейное звено с двумя входами (Мa и Мb) и двумя выходами (a и b). Если ввести обозначения К = 1/Н, Тa=Ja/Н, Тb = Jb/Н, 
, то передаточные
функции этого звена, вытекающие из (32),могут быть записаны в виде:
- по прямым цепям, т.е. от Мa к a и от Мb к b
(33)
- по перекрестным цепям, т.е. от Мa к b и от Мb к a
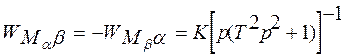(34)
Таким образом, по прямым цепям трехстепенной гироскоп
является колебательным звеном, по перекрестным - интегрирующим колебательным.
Если же ограничиться рамками прецессионной теории, т.е. положить Ja =Jb = 0, то можно установить, что связь по прямым цепям
отсутствует ( 
), а по перекрестным цепям
гироскоп представляет собой интегрирующее звено (
).
Выше были получены передаточные функции трехстепенного гироскопа. Аналогичным образом могут быть получены передаточные функции и других гироскопических приборов, рассматриваемых в последующих разделах.
В заключение обратимся еще раз к передаточным функциям (33), (34), которые свидетельствуют о наличии в движении трехстепенного гироскопа собственных колебаний с круговой частотой n = 1/Т. Как уже выяснено выше, эти колебания есть нутационное движение гироскопа. Если пренебречь наличием подвеса, т.е. положить Ja = Jb = Jэ, то для круговой частоты нутационных колебаний получим выражение
n1 = Н/Jэºn,
выведенное ранее в разделе 1.3. С учетом же инерционности элементов подвеса имеем
.
Таким образом, выявлен важный для практики факт: наличие подвеса гироскопа приводит к снижению частоты нутационных колебаний. Впрочем, этот факт вытекает и из общей теоремы, доказываемой в аналитической механике, согласно которой увеличение масс элементов механической системы приводит к снижению частот собственных колебаний системы.
Еще одно обстоятельство, которое целесообразно отметить в связи с изложенным выше, состоит в следующем. При анализе движения трехстепенного гироскопа не учитывалось наличие (хотя и, как правило, малого) вязкого трения по осям подвеса. Оно приводит к затуханию со временем нутационных колебаний гироскопа. Это обстоятельство является еще одним аргументом в пользу допустимости использования прецессионной теории при решении прикладных задач гироскопии и, прежде всего, задач, связанных с использованием гироскопов в системах управления. Однако, о наличии в гироскопах нутационных колебаний необходимо помнить с тем, чтобы избежать неблагоприятных резонансных явлений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.