Навигационные системы. Часть 1. Гироскопические приборы и устройства навигационных систем: Учебное пособие, страница 17

Уже отмечалось,  что строить плоскость ме-      стного горизонта или, что то же, направление текущей вертикали гироскоп не способен и потому требуются иные устройства.  Простейшим  из  них является маятник. Если точка подвеса маятника неподвижна относительно Земли,  то маятник после успокоения колебаний установится в направлении линии отвеса,  т.е.  местной вертикали. Но если точка подвеса движется с ускорением,  а это  имеет  место при использовании маятника на подвижном объекте,  то его положение в общем случае не будет совпадать с вертикалью, но будет составлять с ней некоторый угол d (рис.19). Выведем уравнение для определения этого угла, полагая, для конкретности, что   ось   качания   маятника    совпадает с осью Ox_г   местной   горизонтальной системы координат. Пусть m - масса маятника,   - его длина,    -  абсолютное ускорение объекта. Проекция  абсолютного ускорения массы m на направление  t, касательное к ее траектории, равна

(производной от  W_x пренебрегаем вследствие ее малости).

Следовательно, уравнение движения m в проекции на  t  имеет вид

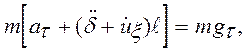
где g_t - проекция ускорения силы притяжения Земли на t. Отсюда имеем

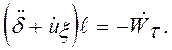                      (36)

Здесь  - проекция кажущегося ускорения точки подвеса  (объекта) на  t, которое при малом  d равно

.                      (37)

Подставляя эту формулу в (36), получим

. (38)

Таким образом,  если маятник помещен на подвижный объект, то он строит вертикаль с ошибкой, величина которой определяется правой  частью уравнения (38).  Возникает весьма важный для практики вопрос:  можно ли подобрать параметры  маятника  так, чтобы исключить эту ошибку? Положительный ответ на этот вопрос был дан еще на  заре  прикладной  гироскопии  немецким  ученым М. Шулером.

Чтобы получить этот  результат,  преобразуем  величину  в правой части уравнения (38), используя соотношение (35) для u_x

.               (39)

Здесь принят во внимание тот факт,  что проекции на горизонтальную ось абсолютного и кажущегося ускорений равны, ибо g_h=0.

Из (39) вытекает, что если длина математического маятника    равна радиусу Земли R,  то маятник  не  реагирует  на  движение объекта. Маятник с указанным свойством называется невозмущаемым. (Заметим,  что  полученный  результат  интуитивно очевиден: если масса m находится в центре Земли,  то как бы не  перемещалась точка О, маятник всегда будет ориентирован по радиусу Земли,  т.е.  по  вертикали  в точке О).  Но реализовать практически такой математический маятник,  очевидно, невозможно. Если  вместо математического взять физический маятник,  то для него результат сохранится при выполнении условия равенства его приведенной длины

                                                                    (40)

радиусу Земли. В (40) J - момент инерции физического маятника, m - его масса,   r - расстояние от центра подвеса до центра масс. Как показывает  анализ,  осуществление физического маятника со свойством невозмущаемости также  не  представляется  реальным.

Однако, невозмущаемый маятник можно реализовать с помощью иных технических средств,  например,  с помощью акселерометра  (А), датчика момента (ДМ) и электронного звена (рис.20).

Уравнение движения основания П изображенного устройства с учетом того, что сигнал акселерометра равен умноженной на коэффициент  передачи  акселерометра величине правой части равенства  (37), таково

            (41)

где J - момент инерции подвижных частей устройства вокруг оси x_г, k - произведение  коэффициентов    передачи    акселерометра  и электронного звена. После преобразования (41) получим уравнение того же вида,  что и (38), если положить

Это дает основание изображенное устройство также  назвать маятником, и этот маятник будет невозмущаемым при  = R,  т.е.  при k = J/R. Это условие в принципе осуществимо.

Заметим, что  круговая  частота собственных колебаний невозмущаемого маятника, как следует из (38), равна .