Метрология и технические измерения отрасли: Лабораторный практикум, страница 13

4.1. Агульныя звесткі

Амаль усе сродкі вымярэнняў (СВ) маюць элементы, якія ва-лодаюць механічнай, цеплавой або іншай інерцыяй, у выніку чаго велічыня сігналу на выхадзе Y(τ) залежыць не толькі ад велічыні ўва-ходнага сігналу X(τ), але і ад яго формы (хуткасці змянення) і часу. Інерцыйныя ўласцівасці СВ вызначаюцца дынамічнымі характарыс-тыкамі, якія апісваюцца дыферэнцыяльнымі ўраўненнямі выгляду

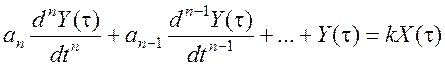               (1)

або адпаведнай перадаткавай функцыяй

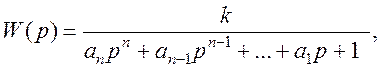                    (2)

дзе a₁, a₂, …, a_n – каэфіцыенты, вызначаныя з пачатковых умоў; k– адчувальнасць СВ.

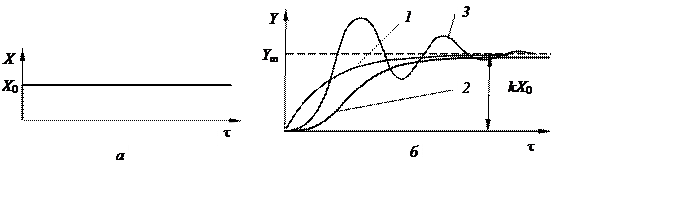
Мал. 4.1. Часовыя характарыстыкі СВ:

а – уваходная велічыня; б – выхадныя велічыні; 1 – аперыядычны ланцуг першага парадку; 2 – аперыядычны ланцуг другога парадку; 3 – хістальнае звяно

У залежнасці ад формы сігналу, які падаецца на ўваход СВ пры даследаванні яго дынамічных уласцівасцей, адрозніваюць часовыя (пераходныя), імпульсныя і частотныя характарыстыкі. Для пабудовы часовай характарыстыкі на ўваход СВ падаецца ступеньчатае ўз-дзеянне, амплітуда якога прынята за адзінку (мал. 4.1а). Форма ча-совай характарыстыкі вызначаецца дынамічнымі ўласцівасцямі СВ і можа мець выгляд, паказаны на мал. 4.1б.

Дынамічныя ўласцівасці тэрмометра залежаць ад яго кан-струкцыі і ўмоў цеплаабмену з навакольным асяроддзем. Калі не ўлічваць  уплыў  корпуса 2 (гл. мал. 4.2), то часовая характарыстыка тэрмометра, усталяванага без ахоўнага чахла, можа быць апісана дыферэнцыяльным ураўненнем першага парадку (крывая 1, мал. 4.1б), рашэннем якога з’яўляецца залежнасць

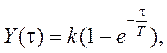                                     (3)

дзе k – адчувальнасць тэрмометра; Т – пастаянная часу, якая прама прапарцыянальна цеплаёмістасці с і масе m адчувальнага элемента і адваротна прапарцыянальна плошчы цеплаабмену F і каэфіцыенту цеплааддачы α вымяраемага асяроддзя да тэрмометра:

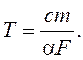                                                          (4)

У шэрагу выпадкаў для прадухілення меха-нічных пашкоджанняў тэрмометры змяшчаюць у ахоўны чахол (мал. 4.2). Аднак гэта пагаршае іх дынамічныя характарыстыкі, што можа быць част-кова кампенсавана запаўненнем прасторы паміж тэрмометрам і чахлом алеем. Дынамічная характа-рыстыка такога тэрмометра апісваецца дыферэн-цыяльным ўраўненнем больш высокага парадку (крывая 2, мал. 4.1б).

Часта атрымаць дакладную дынамічную ха-рактарыстыку аналітычна немагчыма з-за скла-данай узаемнай залежнасці велічынь, якія ўвахо- дзяць у ўраўненне, і яе вызначаюць эксперы-ментальна. Пры гэтым для спрашчэння разлікаў аперыядычныя звёны высокіх парадкаў замяняюць камбінацыяй двух звёнаў – чыстага спазнення і аперыядычнага першага парадку:

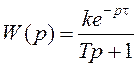                                          (5)

або звёнамі чыстага запазнення і аперыядычнага другога парадку:

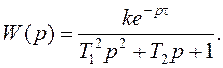                                     (6)

Пры правядзенні эксперымента тэрмометр з асяроддзя з адной тэмпературай хутка перамяшчаюць у асяроддзе з другой тэмпературай і фіксуюць паказанні праз малыя прамежкі часу. Далей атрыманы вынік прыводзяць да безразмернага выгляду

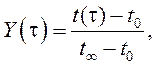                                       (7)

дзе t(τ), t₀ и t_∞– бягучае, пачатковае і новае ўстаноўленае значэнне тэмпературы, і будуюць графік залежнасці Y = f(τ) – пераходны працэс.

Далей па выгляду крывой выбіраюць дынамічную мадэль (5) або (6) і вызначаюць яе пара-метры.

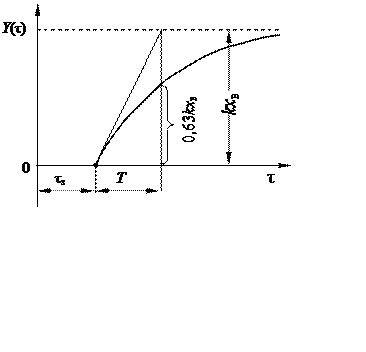
Графічная пабудова датыч-най можа быць выканана са знач-най хібнасцю, таму за пастаянную часу прымаюць час, за які выхад-ная велічыня дасягнула значэння 0,63Y_µ.

Калі пераходны працэс мае выгляд крывой 2 (мал. 4.1б), то могуць быць выкарыстаны залеж-насці і (5), і (6). Датычную да крывой праводзяць у пункце мак-сімальнай хуткасці змены выхадной велічыні (пункт перагібу W) да перасячэння з воссю абсцыс і лініяй, адпаведнай новаму ўсталяванаму значэнню (мал. 4.3).