Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы - импеданс и адмитанс, страница 9

Уравнение движения в комплексном виде

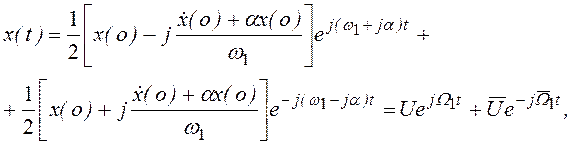                                                                                                                   (3.19)

где     U   и  - комплексные амплитуды; Ω₁ = ω₁ + jα  и  = ω₁ - jα  — комплексные частоты собственных колебаний.

Движение изображено на рис. 3.22.

 

Рис. 3.22. Собственное колебание с затуханием

При очень большом затухании (α > ω₀) движение теряет колебательный характер и становится апериодическим. Степень быстроты затухания собственных колебаний определяется логарифмическим декрементом колебаний

.

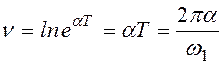Если изобразить движение точки на фазовой плоскости, то получим фазовые траектории не в виде замкнутых кривых, а виде спиралей, накручивающихся на нулевую точку - начало координат (рис. 3.23). Поскольку кривые стремятся сблизиться с нулевой точкой, эта точка, являющаяся положением равновесия, называется положением устойчивого равновесия или устойчивым фокусом.

Если затухание очень велико (α>ω₀), то фазовые кривые, согласно рис. 3.24, асимптотически приближаются к прямой а-а. Характер движения можно получить из следующих равнений:

,        ,

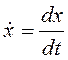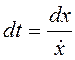откуда                                          ,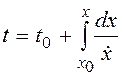

а так как движение в удаленных точках описывается прямолинейными траекториями, то имеем приближенно (для достаточно больших t(х) = - λx, откуда

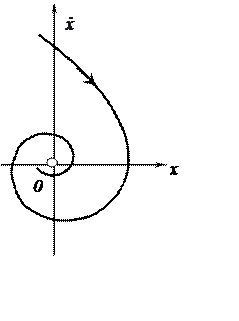
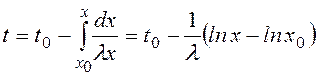,       .                                                                                                                   (3.20)

	Рис. 3.23. Фазовая траектория колебания с затуханием

 

В этом случае нулевая точка называется узлом.

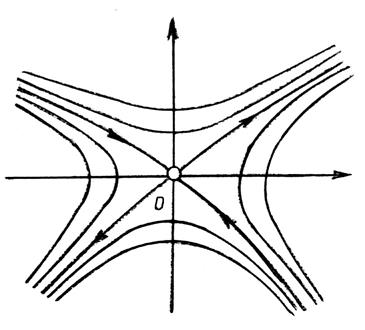
Если в уравнении (3.12) коэффициент с будет отрицательным (отрицательная упругость), то фазовые  траектории располагаются согласно рис. 3.25.   В этом случае имеются две кривые-сепаратриссы (показанные жирной линией), к которым асимптотически приближаются  все траектории; траектории напоминают гиперболы. В этом случае, нулевая точка называется седловой  точкой и изображает неустойчивое положение равновесия. Для линейных колебаний асимптоты прямолинейны, для аналогичного случая при колебаниях с нелинейностью асимптоты имеют, как показано на рис. 3.26, несколько искривленную форму.

					х
	Рис. 3.25. Фазовый портрет линейной системы

 

Наконец, если в уравнении (3.16) коэффициент rположить отрицательным (отрицательное затухание), то фазовые траектории изображаются спиралями, раскручивающимися и удаляющимися от точки О (рис. 3.26). В этом случае нулевая точка называется неустойчивым фокусом.

б)  Вынужденные колебания

Вынужденные колебания возникают в системе при действии внешней периодической силы. При этом в линейной системе гармоническая внешняя сила, имеющая период Т вызывает гармонические колебания с тем же периодом Т.

Если на массу в системе, изображенной на рис. 3.17, будет действовать внешняя сила Р = Р₀ sinωt, то дифференциальное уравнение колебаний будет

                                                                                                                   (3.20)

и движение будет совершаться по закону

.                                                                                                                   (3.21)

При наличии затухания в  системе дифференциальное уравнение колебаний будет

                                                                                                                   (3.22)

и движение совершается по закону

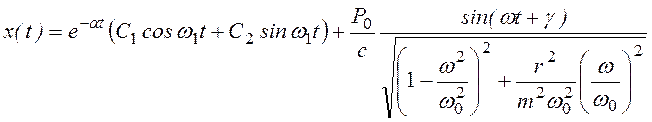,                                                                                                                   (3.23)

,

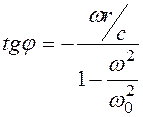где     C₁и С₂ - произвольные постоянные, которые определяются из начальных условий.

В более общем случае, при действии силы Р₀е^jωt, мы по­лучим решение в комплексном виде