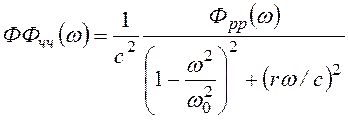Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы - импеданс и адмитанс, страница 12

.                                                                                                                   (3.38)

Последняя формула применяется в тех случаях, когда на систему действует случайная нагрузка, спектральная плотность которой известна на основании измерения с помощью приборов в натуре (примером может служить воздействие неровной дороги на автомобиль).

Зная Ф_xx(ω), можно по известной формуле теории случайных процессов вычислить важную характеристику случайных колебаний - средний квадрат обобщенной координаты (напряжения, деформации, прогиба и т.д.).

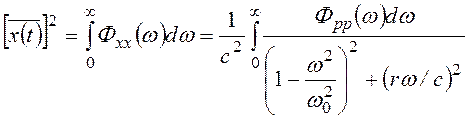.                                                                                                                   (3.39)

При небольшом затухании система с одной степенью свободы реагирует на воздействие сплошного спектра тем, что резонирует при угловой частоте, близкой к ω₀, подобно тому, как это имеет место при действии внешней возбуждающей силы с частотой ω₀.

3.6. Нелинейные колебания

Из систем, совершающих нелинейные колебания, рассмотрим такую, в которой упругая восстанавливающая сила нелинейно выражается через перемещение, причем в том простом случае, когда зависимость между силой и перемещением имеет кубический характер. Такая зависимость часто встречается в различных прокладках и муфтах, где с увеличением перемещения включаются или выключаются дополнительные элементы или связи.

Дифференциальное уравнение колебаний для такой системы имеет вид

.                                                                                                                   (3.40)

Введя безразмерное время , где   , и обозначив штрихами производные по τ, получим

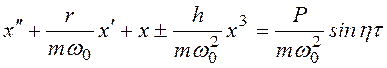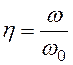,     .                                                                                                                   (3.41)

Движение описываемой системы не является гармоническим. Однако для этой системы при достаточно малом h, как и для многих других подобных систем, колебания близки к линейным, что позволяет их сравнительно легко анализировать.

Предполагая, что движение близко к гармоническому, можно записать приближенное выражение движения в виде

.                                                                                                                   (3.42)

Подставив в уравнение (3.41), получим дифференциальное уравнение, содержащее третью степень от синуса выражения . Достаточно хороший результат получается, если решать уравнение по методу гармонического баланса, одним из вариантов которого является разложение функции в тригонометрический ряд и пренебрежение высшими гармониками.

Имеем

;

.

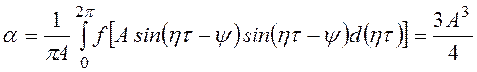Здесь величина а получена как соответствующий член ряда Фурье. Но можно поступить проще: представить куб синуса в следующем виде:

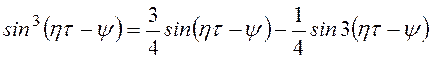                                                                                                                   (3.43)

и непосредственно отбросить второй член, содержащийсинус утроенного угла, что приведет к тому же результату. В результате получим вместо уравнения (3.40) следующее уравнение:

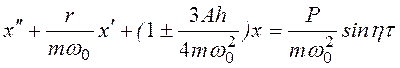                                                                                                                   (3.44)

Теперь подстановка (3.42) дает

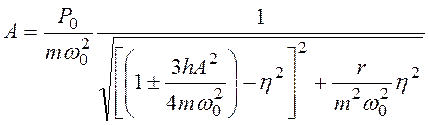,                                                                                                                   (3.45)

.

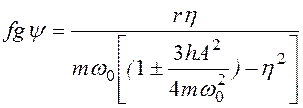Здесь подкоренное выражение в знаменателе зависит от амплитуды А, поэтому выражение (3.45) должно быть решено относительно А. Более удобно, однако, представив зависимость (3.45) в виде

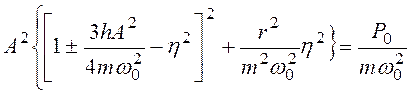,                                                                                                                   (3.46)

разыскивать η как функцию А.

На рис. 3.31 и 3.32 показана зависимость амплитуды от безразмерной частоты для случаев положительного знака и соответственно отрицательного знака перед hв дифференциальном уравнении (3.44). В первом случае амплитудная кривая имеет загиб в сторону увеличивающихся частот, во втором случае она загибается в сторону уменьшающихся частот. Эти случаи соответствуют жесткой и мягкой характеристикам упругой восстанавливающей силы. Пунктирная линия характеризует зависимость усредненной частоты собственных колебаний от амплитуды. Она называется скелетной линией.