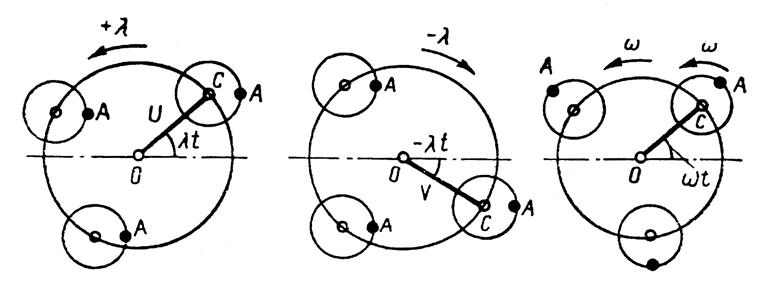|
|
|
|
Рис. 3.60. Составляющие движениявала
Сравнивая вектор неуравновешенности, выражаемой комплексной
величиной 
,с вектором
вынужденных колебаний в формуле (3.103), имеющим выражение
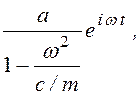
приходим к выводу, что они параллельны, значит ОС и СС' составляют одну прямую линию. Кроме того, при ω < ω0 знаки при величине этих векторов одинаковые, а при ω > ω0 – разные.
Отсюда следует, что при угловой скорости вала ниже критической точки С' лежит вне отрезка ОС, а при угловой скорости вала выше критической точка С' находится внутри ОС.
При неограниченном возрастании ω величина вектора вынужденных колебаний (или радиус, вынужденной круговой прецессии) стремится к нулю. Точка С' стремится совпасть с точкой О. Это есть эффект самоцентровки гибкого вала, выражающийся в уменьшении радиуса вынужденной прецессии диска с увеличением угловой скорости вала.
Во вращающихся валах, как в иных колебательных системах, всегда приступает трение, оказывающее неупругое сопротивление движению. Это сопротивление, обычно способствующее демпфированию, колебаний во вращающихся валах имеет свои особенности: силы сопротивления могут в одних случаях способствовать уменьшению амплитуд, а в других, наоборот, способствовать появлению неустойчивости и неограниченному увеличению амплитуд.
Как известно, трение возникает между телами при их относительном перемещении. Трение, существующее между подвижной частью–валом и внешней средой – неподвижным пространством, назовем внешним трением. Это трение может возникнуть в опорах, а также при наличии специального неподвижного демпфера, соединенного с валом. Оно будет зависеть от абсолютных перемещений точек вала (или скоростей). Другой вид трения – внутреннее трение, возникающее внутри самой вращающейся части, т.е. между частицами материала вала и между валом и напрессованными на него деталями при колебаниях вала и неизбежно происходящих деформациях и скольжениях по поверхностям сопряжения. При таком трении вся система сил сопротивления целиком вращается вместе с валом. Эти силы зависят от относительных перемещений точек вала. В силу сказанного, независимо от закономерности трения, т.е. от характера зависимости сил трения от перемещений или их производных, внешние и внутренние силы трения вызывают силы сопротивления принципиально различного характера.
Действие сил трения зависит от упругих и пластических деформаций и перемещений или их скоростей. Внешнее трение вызывается сопротивлением среды или сопротивлением специальных демпферов. При внешнем трении в большинстве случаев имеет место вязкое сопротивление, т.е. сопротивление, зависящее от скорости перемещения; часто эту зависимость принимают линейной. Внутреннее трение принято описывать с помощью петли гистерезиса при установившемся режиме знакопеременного деформирования. Грубое описание петли дает сухое трение, при котором сила трения постоянна по величинe и изменяет направление с изменением направления деформирования, а, следовательно, знак силы трения зависит от знака относительной скорости. Во многих случаях допустима такая линеаризация внутреннего трения, при которой оно формально подчиняется законам вязкого трения, т.е. пропорционально скорости.
Сказанное позволяет следующее правило для составления выражений силы трения, а именно: а) сила внешнего трения пропорциональна абсолютной скорости перемещения диска, б) сила внутреннего трения пропорциональна относительной скорости перемещения диска, т.е. скорости в той системе координат, для которой вал представляется невращающимся.
Имеем силу внешнего трения в виде
(3.104)
где κ – коэффициент внешнего трения.
Для определения силы внутреннего трения сделаем преобразование движения вала к системе координат, вращающейся с валом с угловой скоростью ω. С этой целью положим
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.