Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы - импеданс и адмитанс, страница 19

Предположим машина (рис. 3.49), масса которой равна т, имеет дополнительно вращающуюся вокруг точки А на плече rмассу m₀, являющуюся возбуждающим фактором. Координаты точки A - , координаты общего центра С массы фундамента и машины — а, b(предполагается, что машина жестко связана с фундаментом). Поместим в центре О подошвы фундамента начало координат, ось х системы направим вправо, а ось у — вверх. Искомое перемещение фундамента выразим тремя величинами: горизонтальным и вертикальным перемещениями х у и поворотом φ вокруг точки О.

 

10

7

8

6

5

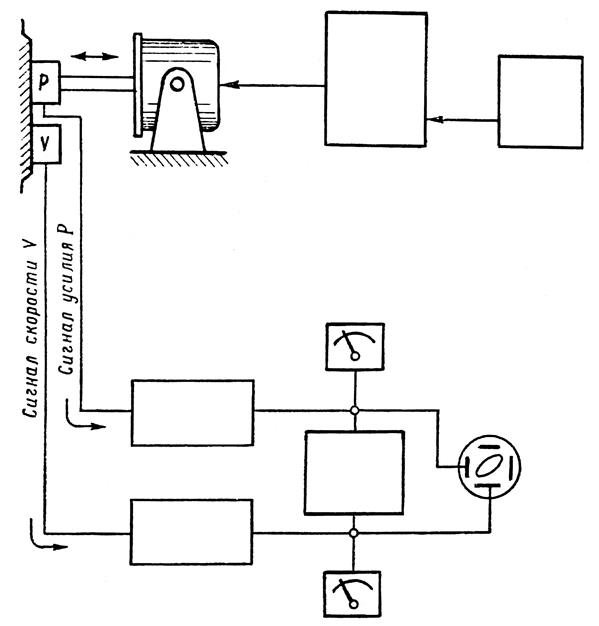
Рис. 3.48. Общая схема установки для опытного определения импеданса:

3 — испытуемый объект;  2 — динамометр; 3 — датчик ускорений 

или скоростей;  4 — электродинамический  вибратор; 5—усилитель;

6 — генератор;  7, 8 — усилители сигналов от датчиков;

9, 11 — вольтметры; 10 — измеритель фазы; 12 — осциллограф

Выбор точки О в качестве начала координат связи с тем что под действием статических сил P_x, Р_yи пары с моментом М фундамент будет совершать перемещения только в направлении этих факторов: горизонтальное, вертикальное и поворот вокруг точки О. Указанное обстоятельство упрощает уравнения колебаний. В данном случае выбранная в качестве начала координат точка основания фундамента является центром упругого сопротивления, а оси x и y— главными центральными осями упругого сопротивления основания.

Для составления уравнений колебаний определим выражения кинетической и потенциальной энергии системы.

 

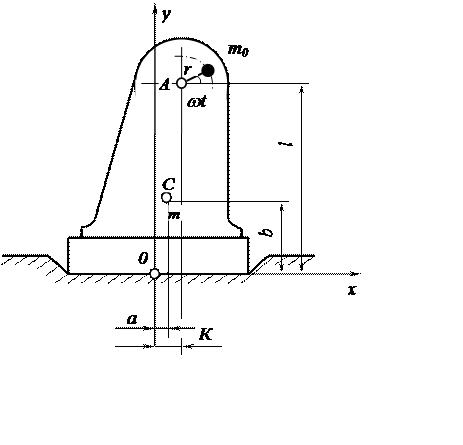Рис. 3.49. Машина с фундаментом на упругом основании

Проекции на оси x, у перемещения и скорости центра тяжести С машины с фундаментом

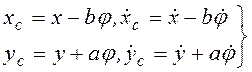.                                                                                                                   (3.68)

Проекции на те же оси перемещения центра sподвижной массы (эксцентрика)

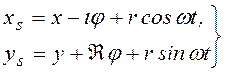.                                                                                                                   (3.69)

Проекции скорости центра подвижной массы

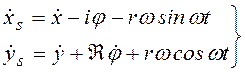.                             (3.7)

Теперь кинетическая энергия двух масс (машина с фундаментом плюс эксцентрик) может быть  представлена выражением

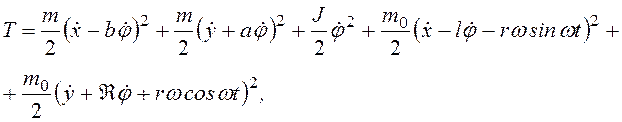                                                                                                                   (3.71)

где     J — момент инерции машины с фундаментом относительно оси, проходящей через точку С перпендикулярно плоскости хy.

Потенциальная энергия деформации основания выражается весьма просто

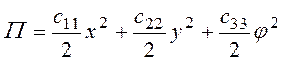.                                                                                                                   (3.72)

Простота этого выражения связана с выбором точки, через перемещения которой определяется потенциальная энергия. Выбранная точка — начало координат и оси, как уже было указано выше, представляют центр и главные центральные оси упругого сопротивления основания, вследствие чего потенциальная энергия выражается через квадраты перемещений. Коэффициенты с₁₁, с₂₂ и c₃₃ — соответственно коэффициенты жесткости основания на оседание, на сдвиги, на поворот вокруг точки О.

Подставив выражение функции Лагранжа L = T— П в уравнения Лагранжа, получим следующие уравнения колебаний машины с фундаментом:

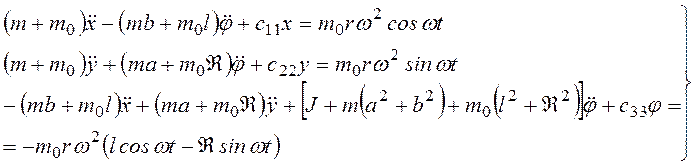(3.73)

В более простом случае, часто встречающемся на практике, когда машина симметрична и расположена на фундаменте симметрично, величины   а   и  обращаются в нуль, уравнения упрощаются

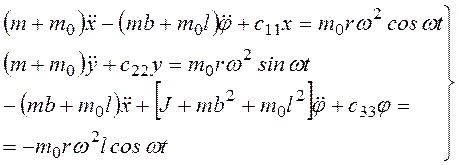.                                                                                                                   (3.74)

Решение этих уравнений будет следующим:

,   ,                                                                                                                      (3.75)

Второе из уравнений (3.74) является независимым; из него получим