Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы - импеданс и адмитанс, страница 24

Вращающийся вал, как упругий стержень, может совершать собственные и вынужденные колебания. Частота его собственных колебаний может, кроме того, зависеть от скорости вращения, в частности, частоты собственных колебаний вращающегося и невращающегося вала различны.

Частота собственных колебаний может увеличиваться и уменьшаться с увеличением скорости вращения. В некоторых случаях частота колебаний совсем не зависит или слабо зависит от скорости вращения вала

Вынужденные колебания вала возникают в результате действия тех или иных периодических возмущений. В большинстве случаев частота возмущения связана с периодом вращения вала и поэтому частота вынужденных колебаний часто бывает кратна числу оборотов вала в единицу времени. При равенстве частот вынужденных и собственных колебаний возникает резонансное или критическое состояние вала, характеризующееся повышенными прогибами. Простейшим и в то же время наиболее часто встречающимся случаем является тот, при котором частота возмущающей силы равна числу оборотов вала. Такой случай имеет место всегда при наличии на валу неуравновешенной массы.

При угловой скорости вала, равной угловой частоте изгибных собственных колебаний вала при данной скорости вращения, возникает критическое состояние вала вследствие неуравновешенности.

Угловая скорость, равная угловой частоте собственных колебаний (при этой же скорости вращения), называется критической скоростью вала.

Здесь нужно отметить, что поскольку угловая скорость вращения вала рассматривается относительно неподвижной системы координат, сопоставляемая с ней угловая частота собственных колебаний должна быть взята также в неподвижной системе координат.

Таким образом, если угловая частота собственных  колебаний λ есть функция скорости вращения, т.е.  λ = λ(ω), то критическая скорость ω₀ выражается соотношением

ω₀ = λ(ω₀)

Обычная неуравновешенность вала вызывает такое колебательное движение, которое приводит к прямой прецессии. При ω = ω₀, т.е. при угловой скорости, равной критической, скорость прецессии равна угловой скорости вала. Такая прецессия называется прямой синхронной прецессией.

В некоторых случаях, как будет в дальнейшем показано неуравновешенность может вызвать обратную прецессию. Поэтому наряду с уже упомянутой критической скоростью, которую можно назвать критической скоростью  прямой прецессии, иногда рассматривают критическую скорость обратной прецессии. Эта величина   удовлетворяет соотношению

.

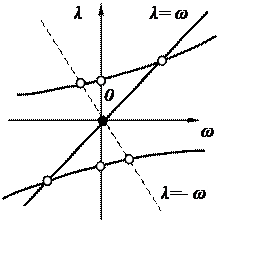
Зависимость угловой частоты λ собственных колебаний валa в неподвижной системе координат от угловой скорости ω можно представить в виде графика, изображенного на рис. 3.58.

На этом графике по горизонтальной оси откладывается угловая скорость ω, по вертикальной оси – угловая частота λ. Функция λ = λ(ω)  изображается  семейством кривых, расположенных, как правило, кососимметрично относительно осей ω, λ. Точки пересечения кривой с осью λ соответствуют угловой частоте собственных колебаний невращающегося вала. Точка пересечения кривой с лучом λ = ω, очевидно, соответствует значениям критических скоростей прямой прецессии, точка пересечения с лучом  соответствует значениям критических скоростей обратной прецессии. Кривая, как правило, состоит не менее чем из одной пары ветвей, а число пар может быть неограниченным. Ветви располагаются кососимметрично (так как  при замене знака одной из величин λ, ω на противоположный прямая прецессия становится обратной и наоборот). Ввиду  этого можно пользоваться либо  правой, либо верхней полуплоскостью (последнее несколько удобнее). В том случае, когда угловая частота λ собственных колебаний вала (в неподвижной системе координат) не зависит от угловой скорости ω, график частоты состоит из прямых, параллельных
оси ω.