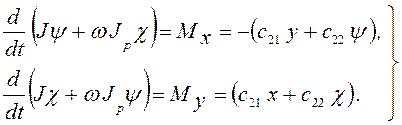Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы - импеданс и адмитанс, страница 28

.                                                                                                                 (3.114)

В формулах (3.113) и (3.114) производные от ωJ_Pψ и –ωJ_Pψ суть гироскопические члены, обращающиеся в нуль при ω = 0, т.е. при отсутствии вращения вала. Они равны с точностью до малых второго порядка проекциям на оси x и у отклоненного вследствие изгиба вала вектора момента количества движения  при вращении вокруг оси s.

Проекции моментов количества движения диска на оси x и у показаны на рис. 3.62,а,б.

В качестве проекций сил и проекций моментов сил в уравнениях (3.113) и (3.114) приняты проекции сил и моментов сил упругости, действующие со стороны вала на диск, пропорциональные соответствующим перемещениям диска. Эти силы выражаются с помощью коэффициентов жесткости с₁₁ , с₁₂ = с₂₁ , с₂₂ , которые имеют такие выражения:

	χ

 

у

S

S

у

χ

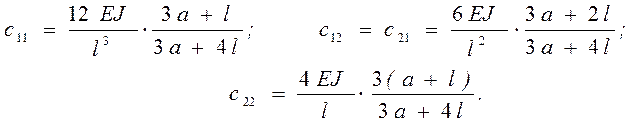
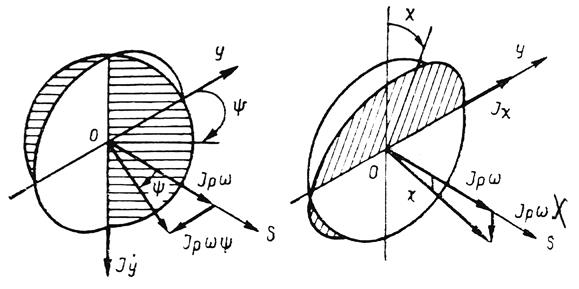
Рис. 3.62. Моменты количества движения диска

Знаки плюс и минус перед коэффициентами жесткости внутри скобок в правых частях уравнений (3.113) и (3.114) соответствуют знакам проекций сил и моментов, действующих со стороны вала на диск согласно рис. 3.63,а,б,в,г.

 

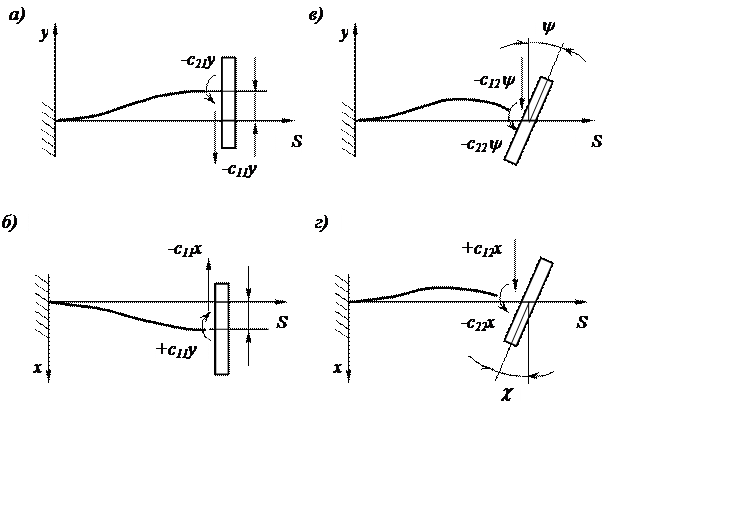Рис. 3.63. Силы, действующие на диск

Из формул (3.113) и (3.114) непосредственно получается система дифференциальных уравнений колебаний вала

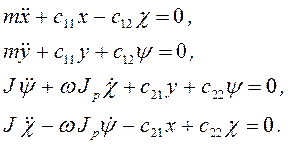                                                                                                                 (3.115)

Сделав замену y – jx= z,   ψ + jχ = 0, а затем, умножив первое и четвертое уравнения на jи сложив со вторым и третьим, получим два комплексных уравнения

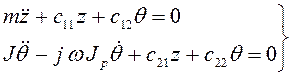.                                                                                                                 (3.116)

Подстановка  z= Ze^jλt,  θ = Θe^jλt в уравнениях (3.116) приводит к алгебраическому уравнению частот

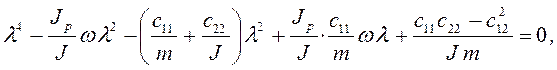                                                                                                                 (3.117)

которое имеет при любом значении ω два положительных и отрицательных корня. Если заменить ω на –ω, то это будет равносильно замене λ на
-λ, а поэтому вся кривая, изображающая зависимость λ от ω, состоит из двух пар ветвей, расположенных кососимметрично относительно осей координат ω, λ. Для полной характеристики кривой достаточно пользоваться одной парой ветвей,  расположенной в положительной области частот, поэтому интервал для угловой скорости ω надо рассматривать от  –∞ до +∞, а интервал собственных частот λ – от 0 до +∞.

Критическая скорость может быть определена, если в уравнении (3.117) положить λ = ω = ω₀, а затем найти корни полученного  уравнения.

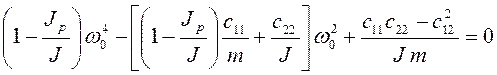.                                                                                                                 (3.118)

Если прикрепленный диск имеет малую толщину по сравнению с его диаметром, то его полярный момент инерции больше экваториального, т.е. J_P > J; тогда уравнение (3.118) будет иметь один вещественный положительный корень, а вал одну критическую скорость прямой прецессии.

Если же прикрепленное к валу тело имеет удлиненную вдоль вала форму, то для него J_P < J, и уравнение (3.118) будет иметь два вещественных положительных корня, в соответствии с чем появятся две критические скорости прямой прецессии вала.

Графики зависимостей λ = λ(ω),  построенные для случаев  J_P = 2J и J_P = J/2,  показаны на рис. 3.64 и 3.65.

При наличии дебаланса вала – смещения а центра дифференциальных уравнений (3.116) будем иметь следующие:

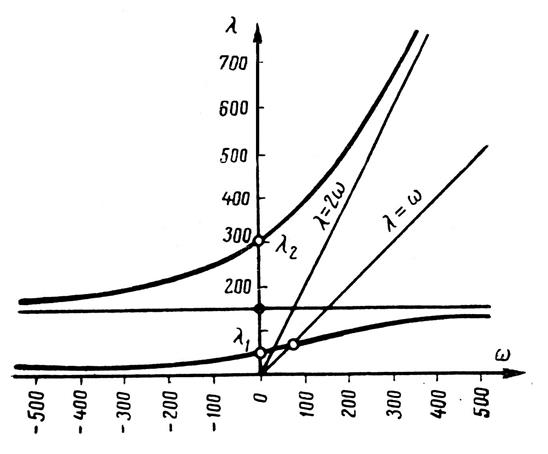
Рис. 3.64. Зависимость между λ и ω для консольного вала

с диском на конце

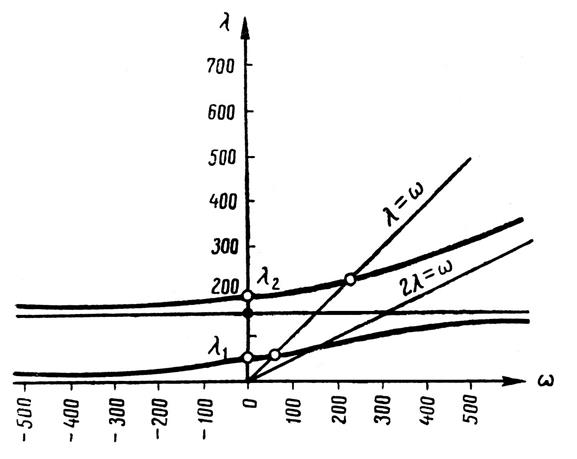
Рис. 3.65. Зависимость между λ и ω  для вала,

имеющего на конце тело вытянутой по оси формы