Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы - импеданс и адмитанс, страница 16

Эти два вида возбуждения отличаются тем, что в первом задана относительная скорость, а во втором — сила. Во многих случаях одна из точек бывает неподвижна, в таком случае имеем дело с возбуждением одной точки системы и величинах импеданса и адмитанса фигурирует абсолютная скорость.

Рассмотрим примеры определения импеданса и адмитанс для простейших систем. На рис. 3.41,а показана система, имеющая последовательно соединенные сопротивление (демпфер и пружину, которая возбуждается силой P = P₀e^jωt.Адмитанс импеданс в точке приложения силы получаются из простых соотношений

,

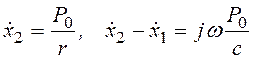откуда, исключая ,находим адмитанс или обратную величину импеданса

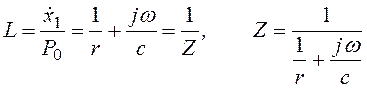,                                                                                                                   (3.62)

откуда следует, что при последовательном соединении элементов адмитанс получается как сумма адмитансов элементов или обратная величина импеданса равна сумме обратных величин импедансов элементов. На рис. 3.41,б изображен в логарифмических координатах модуль адмитанса, а на рис. 3.41,в - его фаза.

 

в)

б)

        

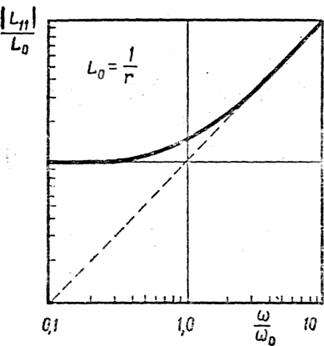
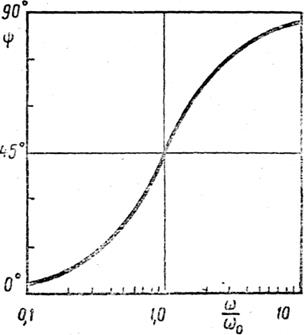
Рис. 3.41. Система из демпфера и пружины и ее адмитанс

Для системы, составленной последовательно из массы, пружины и сопротивления (рис. 3.42,а), аналогично выводится сложением импеданс и сложением   обратных   величин обратная величина импеданса

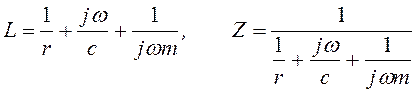                                                                                                                   (3.63)

Модуль и фаза адмитанса показаны на рис. 3.42,б и 3.42,в.

	а)

 

в)

б)

       

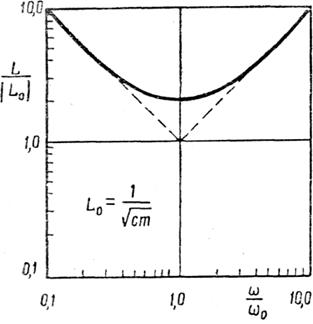
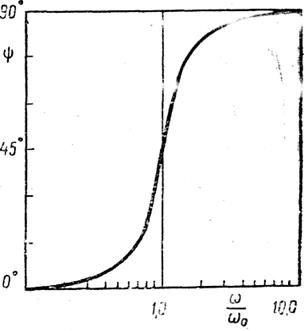
Рис. 3. 42. Система с последовательным соединением элементов:

массы, пружины и демпфера и ее адмитанс

Для системы, образованной параллельным соединением сопротивления, пружины и массы (рис. 3.43,а), как в этом легко убедиться, будем иметь обратные соотношения, а именно: импеданс в точке возбуждения будет равен сумме импедансов элементов или обратная величина адмитанса будет равна сумме обратных величин адмитансов элементов. Таким образом

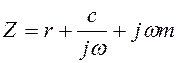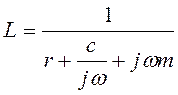,                                                                                                                        (3.64)

На рис. 3.43,б и 3.43,в показаны модуль и фаза адмитанса рассматриваемой системы.

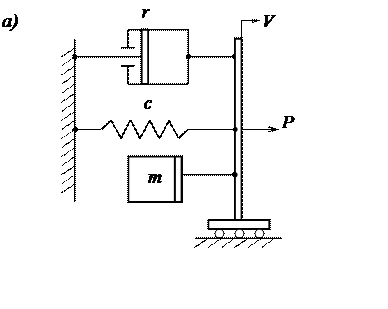
Возможна комбинация из параллельного и последовательного соединения элементов. Система такого типа изображена на рис. 3.44,а, причем эта система идеальная,  без сопротивления.  После простых выкладок смо-

жем найти импеданс

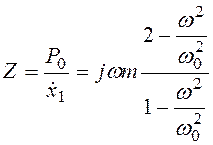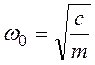,                                                                                                                      (3.65)

 

в)

б)

      

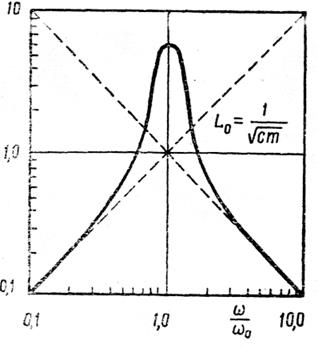
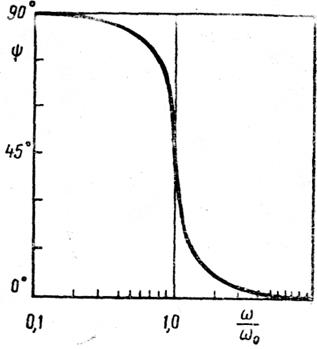
Рис. 3. 43. Система с параллельным соединением элементов:

демпфера, пружины и массы и ее адмитанс

На рис. 3.44,б изображена величина  в  функции  ω²  в обычной системе координат с равномерной шкалой, эта функция имеет два нуля при ω² = 0 и при ω² = 2ω²₀ и один полюс при ω² = ω²₀.

На рис. 3.45,а  изображена  та же система,  но с дополнительно  вве-

денным сопротивлением. Логарифмическое изображение модуля и фазы импеданса дано на рис. 3.45,б и 3.45,в.

Кроме тех величин адмитанса и импеданса, которые определяются для сил и скоростей одной и той же точки, можно определить переходные величины, а именно

,  

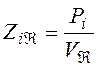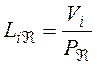
которые легко могут быть определены для рассмотренных выше простейших систем. Эти величины необходимы при составлении выражений импеданса и адмитанса для сложных систем.