Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы - импеданс и адмитанс, страница 11

Наряду с механическими колебаниями существуют колебания в электрических цепях. Они описываются формально теми же дифференциальными уравнениями, что и уравнения для механических колебаний. Это приводит к аналогии уравнений, которая используется в настоящее время для создания электрических установок, описывающих процессы в механических системах.

На рис. 3.30,а изображена колебательная система с одной степенью свободы. Дифференциальное уравнение колебаний этой системы, записанное относительно скорости v—, имеет вид

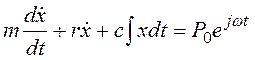.                                                                                                                   (3.34)

На рис. 3. 30,б изображена электрическая цепь, в которую последовательно включены индуктивность L, емкость С и сопротивление R. При подаче в цепь напряжения  колебания тока i в цепи описываются дифференциальным уравнением

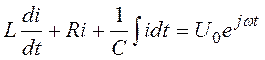.                                                                                                                   (3.35)

Для другой цепи-модели, изображенной на рис. 3.30,в, в которой параллельно включены емкость С, индуктивность Lи проводимость gк в которую подается ток I(t) = I₀e^jωt, колебания напряжения и описываются дифференциальным уравнением

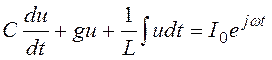.                                                                                                                   (3.36)

Две модели (рис. 3.30,б и рис. 3.30,в) представляют два различных электрических аналога механической колебательной системы, изображенной на рис. 3.30,а, а дифференциальные уравнения (3.35) и (3.36) выражают две системы аналогии уравнения (3.34). Если взять, например, уравнение (3.35), то выбрав значения величин L, Rи С, равными соответствующим значениям величин т, rи 1/cв уравнении (3.34), сможем решить задачу о механических колебаниях с помощью наблюдений над электрической системой. То же самое можно сделать с уравнением (3.36).

Описанные аналогии позволяют указать всю систему соответствия величин, относящихся к механической и электрической системам. В качестве механических величин могут использоваться как линейные, так и угловые перемещения, как силы, так и моменты, т.е. обобщенные координаты и обобщенные силы. Ниже приводится таблица электрических аналогов механических величин по двум системам аналогий.

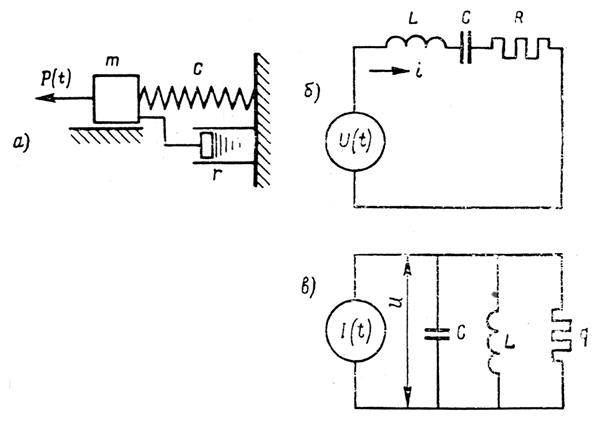
Рис. 3. 30. Механическая колебательная система

и ее электрические аналоги

При действии нагрузки, состоящей из многих гармоник,

колебания системы выражаются формулой

Таблица электрических аналогов механических величин

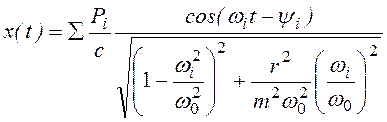.                                                                                                                   (3.37)

При действии на линейную систему случайной нагрузки со сплошным спектром спектральная плотность Ф_xx(ω) обобщенной координаты x(t) для установившихся колебаний выражается через спектральную плотность Ф_pp(ω) нагрузки P(t) формулой