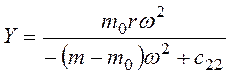Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы - импеданс и адмитанс, страница 20

,                                                                                                                   (3.76)

а из первого и третьего – остальные неизвестные

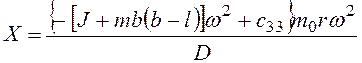                                                                                                                   (3.77)

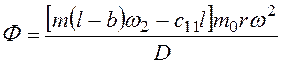                                                                                                                   (3.78)

Формулы (3.76), (3.77), (3.78) несколько преобразуем:

;

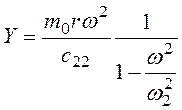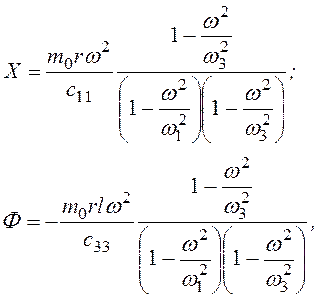
где     ω₁, ω₃ – корни биквадратного уравнения

,

,   ,  

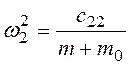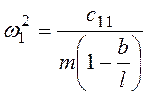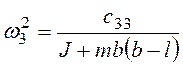
Величины X, Y, Ф — амплитудывынужденных колебаний фундамента под действием вращающегося эксцентрика — неуравновешенного груза. Соотношение этих трех величин определяет форму колебаний, т.е. характер движения общей жесткой конфигурации — машина-фундамент. Очевидно, что указанное соотношение зависит от скорости вращения эксцентрика, т.е. от частоты колебательного возбуждения.

Можно определить для любого момента времени положение центра вращения этой конфигурации как твердого тела. В рассматриваемом частном случае, когда машина с фундаментом симметрична и горизонтальные колебания с поворотными совершаются в одной фазе, координаты центра вращения, будут

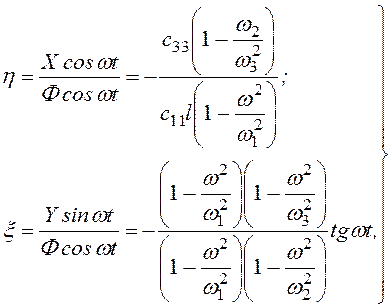
                                                                                                                   (3.79)

откуда ясно, что центр вращения движется по прямой, параллельной оси х. Если, как это может случиться на практике, основание имеет абсолютную жесткость по оси у, то центр вращения будет представлять неподвижную точку на этой оси.

Из формулы (3.79) видно, что положение центра вращения фундамента зависит от частоты вынужденных колебаний, т.е. от скорости вращения эксцентрика.

3.12. Машина и фундамент в виде упруго подвешенного тела

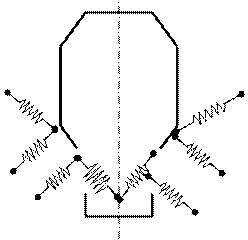
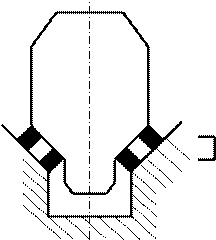
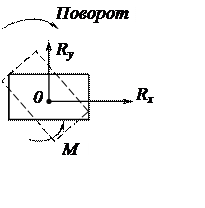
Рассмотрим тот случай, когда машина с фундаментом расположена на системе упругих подкладок или эквивалентной системе упругих стержней (или пружин). Такого типа основание изображено на рис. 3.51 (этот способ подвески встречается, в частности, в конструкциях тепловозных двигателей). Каждая из упругих прокладок имеет свои коэффициенты жесткости (или податливости) на сжатие и на сдвиг, поэтому она может быть схематично изображена в виде двух эквивалентных упругих стержней (или пружин) с коэффициентом жесткости, которые должны быть известны из опыта (рис. 3.52). В результате приходим к схеме твердого тела машина — фундамент, опирающегося на систему деформируемых пружин, подчиняющихся тому или иному закону деформирования в зависимости от действующего усилия. Нередко закон выражается нелинейной зависимостью, но во многих случаях в известных пределах он может быть принят линейным. Тогда в изображенной системе имеется центр и главные оси упругой подвески.

Пусть машина и система упругих прокладок будут симметричны.

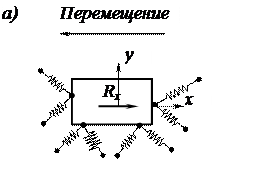
Главные оси и центр упругости подвески расположены согласно рис. 3.53. Их можно найти на основании правила сложения сил, действующих в плоскости, вызванных поступательными перемещениями тела в направлении осей х и у; соответствующие равнодействующие будут (рис. 3.54).

,    ,                                                                                                                   (3.80)

где     с_i — коэффициенты жесткости пружин, a α_i — углы наклона осей пружин к оси  х. Точка  О  пересечения R_xи R_у определит положение начала координат, так как является центром поворота тела при действии пары см в плоскости  ху.

Рис. 3.51.  Схема машины с фундаментом на упругих прокладках

Рис. 3.52. Имитация упругих прокладок с помощью пружин

б)

в)

Рис. 3.53. Схема упругого сопротивления смещению фундамента

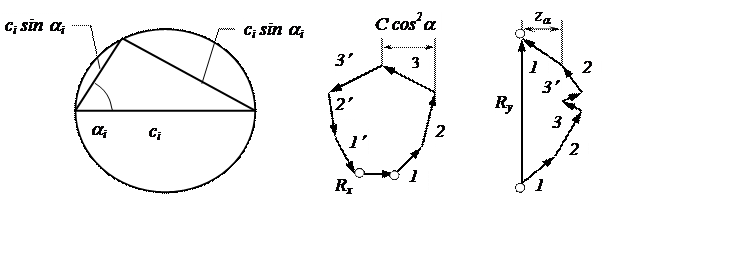Рис. 3.54. К определению главных центральных, осей упругой подвески