Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы - импеданс и адмитанс, страница 4

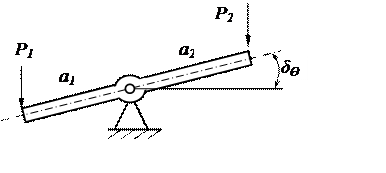
δW = P₁α₁δθ - Р₂α₂δθ = (P₁α₁- Р₂α₂) δθ = M δθ,

откуда следует, что обобщенной силой, соответствующей обобщенной координате θ, будет пара сил с моментом

M= P₁α₁ - Р₂α₂.

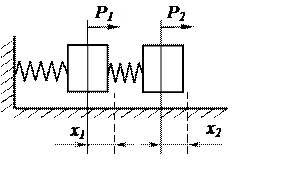
            Рис. 3.5.   Обобщенные силы           Рис. 3.6. Обобщенные силы

для системы с двумя                           для рычага

степенями свободы

При анализе и расчетах колебательных систем используют как классические методы механики, так и специальные практические методы, часто обладающие значительной эффективностью применительно к колебательным системам.

Из классических методов механики употребительны способ, основанный на применении теорем о количестве движения и о моменте количества движения, метод кинетостатики и метод Лагранжа. Метод кинетостатики дает хороший способ составления дифференциальных уравнений движения в простейших случаях, когда система достаточно обозрима и имеется возможность простого составления уравнений движения в форме уравнений равновесия точек системы, находящихся под действием внешних сил и сил инерции в абсолютном движении. В более сложных случаях применение этого метода затруднительно.

Наиболее общим является метод Лагранжа, использующий обобщенные координаты и обобщенные силы. Принимая в качестве неизвестных обобщенные координаты, на основании этого метода составляется система дифференциальных уравнений вида

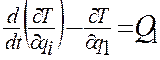.                                                                                                                     (3.1)

Число таких уравнений равно числу степеней свободы системы.

Для систем с упругими силами вводится потенциальная энергия П, для которой

Q^y_i =

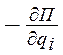
и уравнения Лагранжа (3.1) переписываются в виде

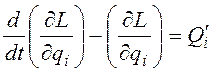,                                                                                                                     (3.2)

где     L= T- П – функция Лагранжа;

 – сила, из которой вычтена сила упругости.

При наличии сопротивления, вызывающего рассеяние энергии в системе, в простейших случаях силы сопротивления выражаются через диссипативную функцию Ф

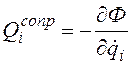.                                                                                                                     (3.3)

Практические методы решения задач теории колебаний основаны либо на „угадывании" всей совокупности обобщенных координат и последующем уточнении с помощью последовательных приближений (прямые методы, методы последовательных приближений), либо на построении для частей системы некоторых выходных динамических характеристик. С помощью таких характеристик последовательным „наращиванием" определяется динамическая характеристика целой системы, а также определяются ее необходимые свойства.

Практическим преимуществом указанных эффективных методов перед классическими является то, что классические методы позволяют только составить дифференциальные уравнения движения, а эти методы дают возможность получить решение задачи без составления уравнений.

3.2.  Кинематика колебаний  и   возбуждающие нагрузки

При колебаниях деталей машин или механизмов отдельные точки совершают колебательное движение. Простейшим колебательным движением является гармоническое колебание, которое аналитически выражает перемещение как функцию времени

x(t) = a cos(wt + φ)                                                                                                                     (3.4)

или                                           y(t) = a sin(wt + φ).                                                 (3.5)

Оба эти движения можно получить следующим образом. Если представить себе некоторую точку A, равномерно движущуюся по окружности радиуса а, при угловой скорости радиуса, равной ω, то выражения (3.4) и (3.5) будут представлять собой проекции перемещения точки А на оси х и у (рис. 3.7). Гармоническое колебание — движение периодическое, так как перемещения точки возвращаются к первоначальным значениям по истечении времени Т, 2Т , 3T,...,nТ, где Т— период обращения точки, с; n — целое число.