x(t) = U![]() , (3.14)
, (3.14)
где величины Uи Vимеют выражения:
U = 1/2(x(0)- j![]() (0)/ω0), V = 1/2(x(0)+ j
(0)/ω0), V = 1/2(x(0)+ j![]() (0)/ω) (3.15)
(0)/ω) (3.15)
и представляют собой комплексные амплитуды.
Уравнение колебаний в записи
(3.14) геометрически интерпретируется движением конца вектора — суммы,
слагаемыми которого являются векторы ![]() и
и ![]() , имеющие постоянную длину (модуль) и вращающиеся с угловой
скоростью ω0 — первый против часовой стрелки, второй по часовой
стрелке.
, имеющие постоянную длину (модуль) и вращающиеся с угловой
скоростью ω0 — первый против часовой стрелки, второй по часовой
стрелке.
Формулы (3.13) и (3.14) выражают колебательное движение как функцию времени. Движение изображается кривой на рис. 3.19.
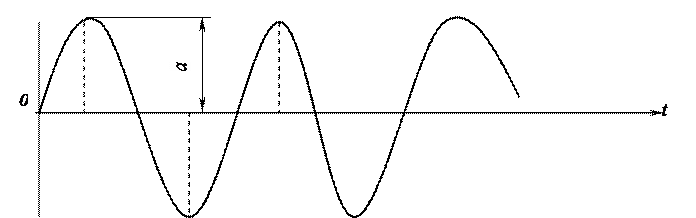 |
Рис. 3.19. Собственное колебание без затухания
Наряду с такими выражениями пользуются так называемым фазовым изображением движения, характеризующим зависимость скорости колеблющейся точки от ее перемещения. При таком изображении время совсем не участвует как параметр, от которого зависит движение.
Если записать выражение перемещения точки и ее скорость
x(t) = asin(ω0+φ),
![]() (t) = ω0 acos(ω0+φ),
(t) = ω0 acos(ω0+φ),
то можно легко получить зависимость
((x(t))2
/a2) + (![]() (t)) 2/(ω0a)
2 = 1, (3.16)
(t)) 2/(ω0a)
2 = 1, (3.16)
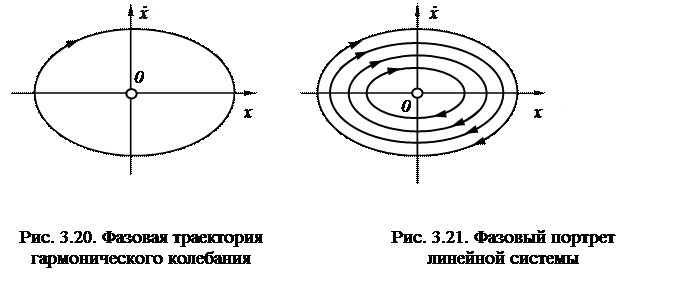
из которой видно, что зависимость между скоростью и перемещением при гармоническом колебании представляет уравнение эллипса, что геометрически показано на рис. 3.20.
Плоскость (х, ![]() ) называется фазовой плоскостью; кривые, изображающие зависимость
скорости от перемещения, называются фазовыми кривыми, или фазовыми
траекториями.
) называется фазовой плоскостью; кривые, изображающие зависимость
скорости от перемещения, называются фазовыми кривыми, или фазовыми
траекториями.
При изменении начальных данных, в частности, амплитуды а, меняются полуоси эллипса. Для различных значений амплитуды будем иметь семейство эллипсов (рис. 3.21).
Полная система фазовых траекторий, изображенных на фазовой плоскости, называется фазовым портретом колебательной системы.
Отметим некоторые свойства фазовых траекторий:
а) движение точки совершается по направлению, показанному на рис. 3.21 стрелками; б) для периодических колебаний, совершающихся с постоянной амплитудой, фазовые траектории представляют замкнутые кривые; в) для гармонических колебаний время совершения одного полного обхода каждой траектории семейства одно и тоже и равно периоду колебаний
T = 2π/ω0 = 1/f.
 |
Рассмотренная колебательная система, энергия которой не увеличивалась и не уменьшалась в процессе движения (за счет притока извне или рассеяния энергии). Такая система является консервативной. При наличии источников сопротивления внешней среды или со стороны деформируемого материала (пружины) колебания происходят таким образом, что за каждый период уменьшается энергия системы, и каждое последующее колебание по сравнению с предыдущим имеет уменьшенную амплитуду. Такое явление называется затуханием собственных колебаний.
Простейшей закономерностью затухания является линейная, когда сила сопротивления пропорциональна скорости движения. В этом случае
диссипативная функция будет
Ф = 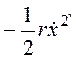 ,
,
а ее производная по ![]() , т.е. сила сопротивления, будет равна r
, т.е. сила сопротивления, будет равна r![]() . Внеся в правую часть уравнения колебаний (3.8) это выражение силы,
получим для системы, совершающей продольные колебания
. Внеся в правую часть уравнения колебаний (3.8) это выражение силы,
получим для системы, совершающей продольные колебания
m![]() + r
+ r![]() + cx = 0 (3.16)
+ cx = 0 (3.16)
и аналогично для системы, совершающей крутильные колебания,
![]() . (3.17)
. (3.17)
Ввиду полной аналогии уравнений (3.16) и (3.17) рассмотрим только уравнение (3.16), интегрирование которого дает движение массы — затухающее колебание
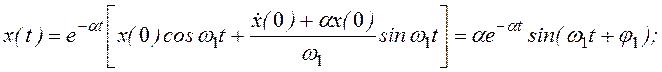 (3.18)
(3.18)
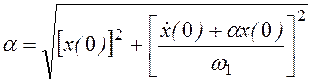 ,
,
где х(0) и ![]() (0) — начальные отклонения и скорость; φ1
— начальная фаза;
(0) — начальные отклонения и скорость; φ1
— начальная фаза; ![]() - угловая частота собственных
затухающих колебаний;
- угловая частота собственных
затухающих колебаний;
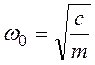 ,
, 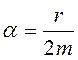 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.