Используя теперь уравнения (3.76) для указанной системы координат, сможем найти значение перемещений при движении эксцентрика.
Выбрав надлежащим образом расположение упругих пружин и их коэффициенты жесткости, необходимо добиться того, чтобы центр упругой подвески совпал с центром тяжести С твердого тела машина — фундамент.
При таком условии формулы для амплитуд симметричной системы (3.77), (3.78) упростятся:
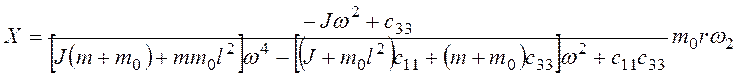; (3.81)
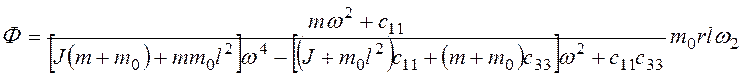. (3.82)
Расстояние до центра вращения
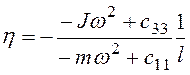(3.83)
Значения усилий в упругих пружинах выражаются следующей формулой:
, (3.84)
где di– длины перпендикуляров из центра О на оси пружин. Подставив вместо X, Y, Ф их значения из общих формул (3.76), (3.77) и (3.78) для симметричной системы, получим
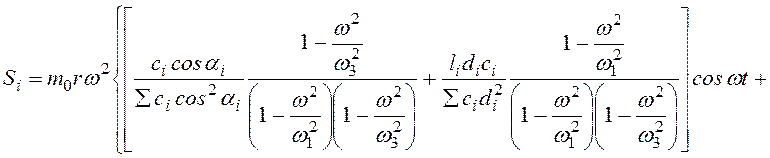
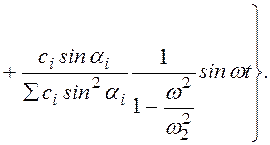(3.85)
Здесь были рассмотрены такие системы, в которых машина с фундаментом и основание, т.е. система упругих пружин, обладают одной осью симметрии. В этих системах центр упругого сопротивления лежит на оси симметрии, а ось является одновременно одной из главных осей упругого сопротивления. Если система упругих пружин не имеет симметрии, то центр и главные оси упругого сопротивления все же существуют, однако определение их более сложно. Не развивая подробно этот вопрос, укажем в общих чертах, что можно определить центр и главные оси упругого сопротивления для несимметричной системы. Используя эти оси в качестве осей координат, можно составить общие уравнения колебаний, подобные уравнением (3.73).
3.13. Изгибные колебания вращающихся гибких валов.
Элементы колебательного движения гибкого вала
В качестве примера собственных и вынужденных стационарных колебаний рассмотрим изгибные колебания гибких валов, специфической особенностью которых является наличие вращения. В этих колебаниях предоставляет интерес как собственно процесс колебаний, выражающийся в комбинации гармонических движений и вращения, так и те угловые скорости на которых возникают повышенные прогибы вала, нередко сопровождающиеся поломкамииными словами, критические скорости вращения.
Литература, касающаяся вопросов изгибных колебаний гибких валов, в течение нескольких десятилетий своего существования (до 50-х годов текущего столетия) в подавляющей своей части относилась к определению частот собственных колебаний и критических скоростей вращения валов. Это отражало определенную направленность исследований, которая в свое время была связана с решением основной задачи — отстройки вала от резонансных состояний. Такая задача вытекала из требований, соответствовавших определенному уровню развития техники, и для обеспечения надежной работы валов ее решение на том этапе являлось достаточным. Однако в настоящее время создание мощных паровых и газовых турбин, турбогенераторов, насосов большой производительности с весьма гибкими валами, прядильных веретен, работающих со скоростями, намного превышающими критическую, а также постройка и использование быстроходных машин ставят задачи обеспечения прочности и устойчивости, которые требуют для своего решения изучения процесса колебательного движения.
Наличие разнообразных источников возбуждения колебаний различной интенсивности и частоты, а также влияние фактора рассеяния энергии требуют анализа, в котором были бы связаны между собой действующие нагрузки (в том числе и силы трения) с колебательным процессом, с одной стороны, и колебательный процесс с напряжениями вала, с другой стороны. Начиная приблизительно с 50-х годов, в литературе появляются работы, в которых освещаются вопросы движения вала, его устойчивости, нестационарного перехода через критические скорости, роли упругой податливости опор и др.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.