Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы - импеданс и адмитанс, страница 15

Используя соотношения (3.56) и выражения (3.54) видим, что при главных колебаниях имеют место соотношения

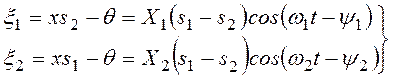                                                                                                                   (3.57)

Координаты ξ₁ и ξ₂ принятые в качестве обобщенных координат, называются главными, или нормальными координатами. Для них система дифференциальных уравнений распадается на два независимых уравнения

,                                                                                                                      (3.58)

Формы колебаний, соответствующие главным координатам, обладают свойством, называемым ортогональностью. Составим выражение

,

где     (х₁, θ₁) и (x₂, θ₂) — значения  координат x, θ, соответствующие главным колебаниям.

На основании (3.57) можем написать

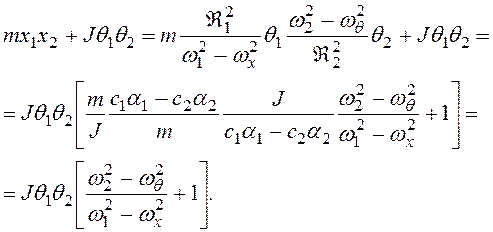
Легко видеть, что выражение в квадратных скобках равно нулю, так как из свойства квадратного уравнения (3.51)

.

Откуда                        

и, следовательно,

,                                                                                                                   (3.59)

что выражает свойство ортогональности форм главных колебаний.

3.8.  Связанные собственные  и вынужденные колебания

систем со многими  степенями свободы.

Динамические характеристики простейших

механической системы и ее элементов

В подразделе 3.7 были описаны некоторые общие свойства, характеризующие связанность колебаний на примере системы, с двумя степенями свободы. При определении частот и форм связанных собственных колебаний систем с большим числом степеней свободы общие классические методы, основанные на составлении частотных уравнений, становятся громоздкими и не дают возможности легко получить практические результаты.

Для анализа таких систем в настоящее время используются специальные, достаточно эффективные методы. К таким методам относится метод, основанный на применении импеданса и адмитанса. При применении этих методов сложная колебательная система расчленяется на ряд более простых или простейших, для каждой из которых определяется динамическая характеристика — импеданс или адмитанс, а затем с помощью этих характеристик производится наращивание-присоединение одной системы к другой до тех пор, пока не будет составлена вся система полностью.

Рассмотрим динамические характеристики механической системы, связанные с действием на нее обобщенного гармонического возбуждения, которое характеризуется зависимостями силы и скорости от времени

P = P₀ e^jωt,   V = V₀e^jωt                                                                                                                    (3.60)

Представим оба вида возбуждения, которые можно характеризовать как силовое и кинематическое возбуждение. В первом из них задана сила с фиксированной амплитудой, во втором — смещение с постоянной амплитудой скорости.

Рассмотрим системы, состоящие из отдельных элементов: рис. 3.39, а — масса т, рис. 3.39, б — элемент с трением, коэффициент rкоторого пропорционален скорости, рис. 3.39, в — упругий элемент с коэффициентомжесткости с. При возбуждении гармонических колебаний этих элементов имеются для них соответственно динамические характеристики —импеданси адмитанс — отношение силы к скорости и наоборот:

 

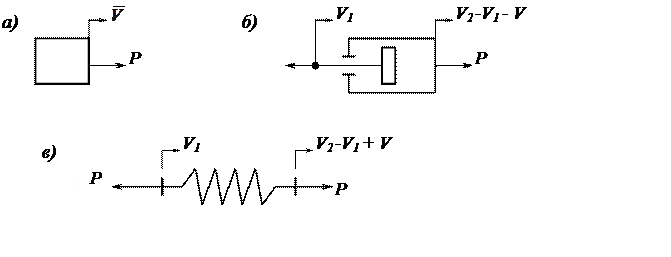Рис. 3.39. Масса, элемент с трением и упругость

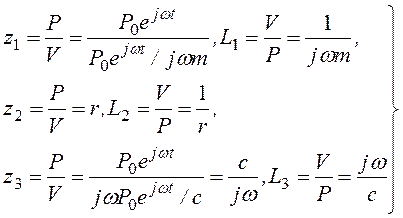.                                                                                                                   (3.61)

Простые зависимости (3.30, 3.31), которые сводятся к прямой и обратной пропорциональности и к константе, легко представить в логарифмическом масштабе в виде прямых линий (рис. 3.40, а, б, в).

Обобщенное кинематическое возбуждение — это такое возбуждение

пары точек системы, при котором этим точкам задано движение с относительной скоростью, равной V₀e^jωt.

         

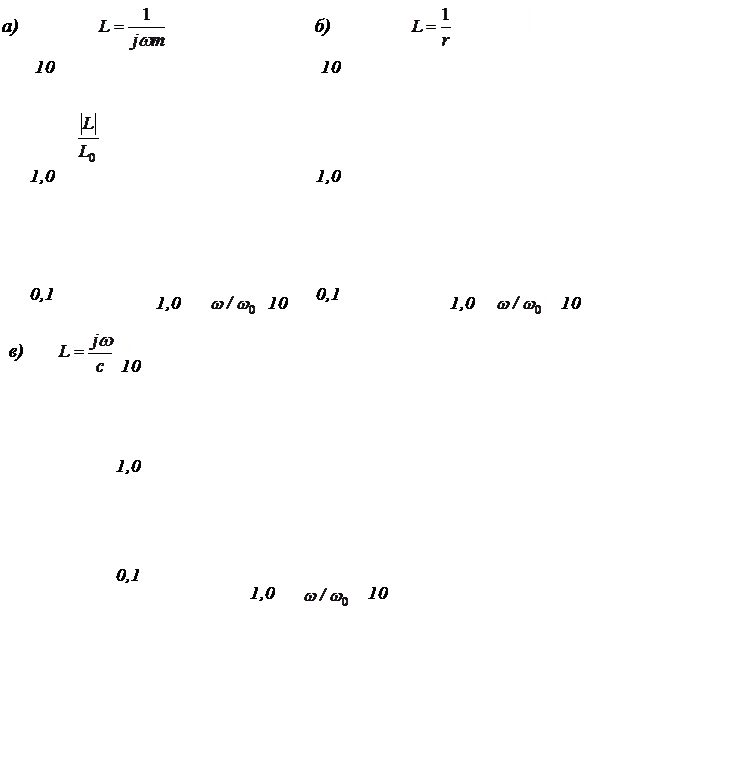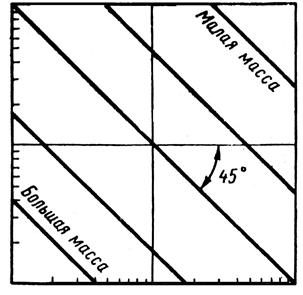
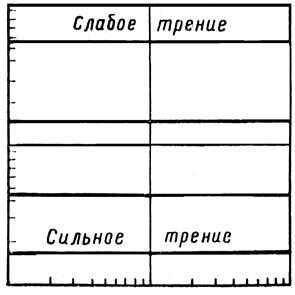
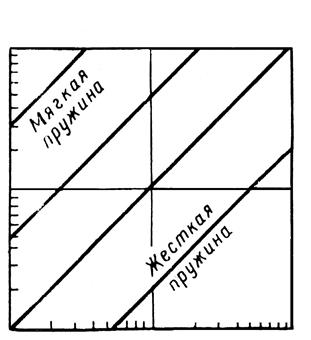
Рис. 3.40. Адмитансы массы, демпфера и пружин

Обобщенным силовым гармоническим - возбуждением системы называется возбуждение какой-либо пары точек системы двумя равными и противоположно направленными силами P₀e^jωt и -P₀e^jωt.