Для очень широкого круга задач о колебаниях в машинах существующие нелинейные зависимости могут быть приближенно заменены линейными. Такая замена возможна, однако, лишь в тех случаях, когда фактическая нелинейность не приводит к существенным явлениям, выпадающим из рассмотрения при линейной трактовке задачи.
Возможна и такая идеализация, при которой те или иные величины, характеризующие свойства элементов, периодически изменяющиеся во времени, полагают в первом приближении постоянными, равными средним значениям этих величин за период. Например, приведенный момент инерции маховика кривошипно-шатунного механизма является периодической функцией, так как его значение зависит от угла, характеризующего положение кривошипа. Но эту величину весьма часто принимают за постоянную. Если же учесть переменность момента инерции маховика в зависимости от указанного угла поворота, то система усложняется и вместе с этим усложняется математическое описание движения.
В результате указанных идеализаций приходим к некоторой механической колебательной системе, отражающей те свойства реальной машины или механизма, которые мы считаем наиболее существенными. При желании можно учесть большее число перемещений элемента машины, при этом для того же реального объекта построим другую, более сложную идеализированную схему, в которой будет отражено большее число свойств объекта, однако и эту схему в дальнейшем можно усложнить. Таким образом, механическая колебательная система есть результат некоторой абстракции, т.е. отвлечения от ряда свойств реального объекта, которая поддается качественному и количественному анализу, т.е. позволяет применить к ней математические методы.
Степень идеализации (или схематизации), до которой должна быть доведена система, чтобы она правильно отражала свойства реального объекта, зависит от требований к точности анализа объекта. Правильность выбора системы, конечно, зависит от опыта и искусства исследователя.
Критерием правильности выбора системы всегда является опыт.
Для теоретического анализа системы, прежде всего, необходимо установить структуру системы. Структура системы определяется количеством ее степеней свободы - числом независимых величин (параметров), через которые может быть выражено любое допустимое перемещение системы.
 Эти величины называются обобщенными
координатами и обозначаются через q1, q2, ,…, qn. В качестве обобщенных координат
принимают как линейные, так и угловые перемещения. Различают системы: а)
дискретные, обладающие конечным числом степеней свободы и
Эти величины называются обобщенными
координатами и обозначаются через q1, q2, ,…, qn. В качестве обобщенных координат
принимают как линейные, так и угловые перемещения. Различают системы: а)
дискретные, обладающие конечным числом степеней свободы и
б) сплошные (непрерывные), обладающие бесконечным числом степеней свободы.
Приведем примеры. Положение плоского тела А, присоединенного к основанию
звеном с шарнирными парами (рис. 3.3), можно охарактеризовать двумя углами α и β.
Но это можно сделать с мощью других величин, а именно xи δ (при условии ограничения движения в первом квадранте) (рис. 3.4).
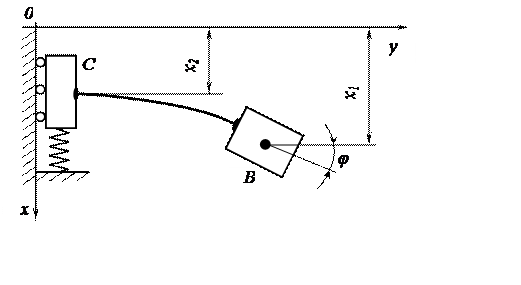
Рис. 3.4 Система с тремя степенями свободы
Приведенные параметры относятся к системам с конечным числом степеней свободы. В этих системах всегда имеется конечное число тел, принимаемых за абсолютно твердые, и конечное число элементов (связей), их соединяющих. Эти связи бывают упругими, неупругими, вязкими и др.
Для деформируемого стержня с распределенной массой нельзя указать число степеней свободы, ибо в каждом ее элементе возможны деформации (изгиба, растяжения-сжатия, сдвига и крушения). Поэтому число форм, которые способен принять стержень в результате деформирования, не ограничено, и система имеет бесконечное число степеней свободы.
Наряду с обобщенными координатами для систем, находящихся под действием внешних сил, рассматривают обобщенные силы, соответствующие координатам. Установление обобщенной силы, соответствующей данной обобщенной координате, иногда весьма просто, но иногда вызывает трудности. Например, если для системы, состоящей из двух масс m1и т2 с пружинами (рис. 3.5), за обобщенные координаты принять перемещения x1 и x2, то обобщенными силами будут силы P1 и Р2, непосредственно действующие на массы в направлении указанных перемещений. Для системы, изображенной на рис. 3.6 (рычаг), на которую действуют две силы P1 и Р2, за обобщенную координату можно принять угол θ, а обобщенная же сила получается из следующего: элементарная работа сил P1 и Р2 на угловом перемещении δθ будет
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.