Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы - импеданс и адмитанс, страница 25

Наряду с графиком  используется изображение зависимости
μ = μ(ω) в подвижной системе координат. Эта зависимость легко получается от предыдущей на основании соотношения μ = λ – ω. Такой график схематически показан на рис. 3.59. Точки пересечения кривой μ = μ(ω), с осью μ изображают частоту невращающегося вала; точки пересечения этих кривых с осью ω − критические скорости, так как в подвижной системе координат критическая скорость соответствует нулевому значению одной из частот собственных колебаний вала.

3.15.  Вал на двух опорах с диском в середине

Рассмотрим колебания вращающегося с угловой скоростью ω вала на двух опорах с диском массы m,расположенным точно в середине между опорами (рис. 3.55). Пусть точка О изображает след оси опор вала, точка С − точку прикрепления диска к гибкому валу (центр диска), точка С' – центр массы диска. Расстояние ОС есть величина прогиба вала посередине;
СС' = а есть величина смещения центра массы диска относительно точки прикрепления диска.

Представим неподвижную систему координат с осями x и началом О. Обозначим угол между вектором СС' и осью y через φ; координаты центра массы диска будут x, y.Предварительно рассмотрим движение без учета трения.

Кинетическая энергия системы будет иметь выражение

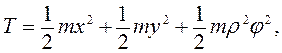                                                                                                                   (3.98)

где     ρ – радиус инерции диска.

Потенциальная энергия изгиба вала, учитывая, что проекции на оси x и y прогиба вала будут соответственно

выразится следующим образом:

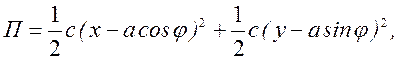                                                                              (3.99)

где     c = 48EJ/l³ – статическая жесткость вала на изгиб сосредоточенной силой в точке прикрепления диска.

Составив выражение функции Лагранжа и вставив ее в уравнение Лангранжа, придем к таким уравнениям:

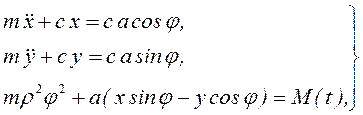                                                                                                                 (3.100)

где     М(t) – внешний момент, приложенный к валу.

Уравнения (3.100) достаточно сложны, и их интегрирование  в общем случае представляет трудную задачу. Однако в обычных случаях оказывается, что угловая скорость вращения вала и, следовательно, вектора неуравновешенности близка к постоянной, а угол φ может быть принят с большой точностью равным ωt. Это сразу же приводит к большим упрощениям: первые два уравнения системы (3.100) становятся независимыми, а третье упрощается.

Система приобретает вид

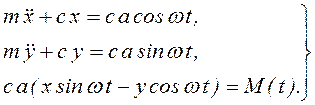                                                                                                                 (3.101)

Первые два уравнения легко интегрируются, а после подстановки значений x и y в третье уравнение момент М(t), поддерживающий данное движение, становится вполне определенным.

Для наглядного представления движения введем комплексную плоскость zи рассмотрим движение центра массы диска, изображаемого концом вектора   z= x + jν.   Умножив второе уравнений (3.101) на и

сложив с первым, получим комплексное уравнение

                                                                                                                 (3.102)

интегрирование, которого дает

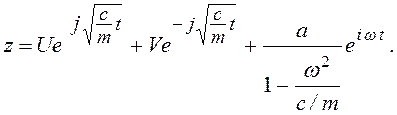                                                                                                                 (3.103)

Движение, описываемое формулой (3.103), представляет комбинацию собственных и вынужденных колебаний. Два первых члена суть прямая и обратная прецессии, совершающиеся с угловой скоростью, равной частоте собственных колебаний вала; коэффициенты U и V зависят от начальных данных движения. Третий член представляет чисто вынужденное колебание – круговую прецессию с угловой скоростью ω вала.

Если  , то значение третьего члена становится неограниченным. Соответствующее значение угловой скорости ω будет критической скоростью вала. В данном простейшем случае частота собственных колебаний не зависит от скорости вращения.

Движения, характеризуемые тремя членами выражения (3.103), показаны на рис. 3.60, а,б,в.