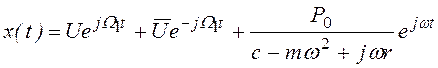 . (3.24)
. (3.24)
В обоих случаях (при отсутствии затуханий и при наличии затуханий) движение состоит из собственных и чисто вынужденных колебаний.
При отсутствии затухания, если частота внешней силы становится равной частоте собственных колебаний системы, третье слагаемое (3.21), выражающее чисто вынужденное колебание, приобретает неограниченное значение и, значит, решение в виде стационарного колебания с постоянной амплитудой теряет смысл. На самом же деле при ω = ω0 вынужденное движение описывается выражением
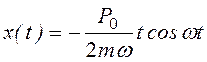 (3.25)
(3.25)
и представляет собой сдвинутое по фазе на π/2 по отношению к возмущающей силе нестационарное колебание с неограниченно возрастающей по линейному закону во времени амплитудой.
При наличии затухания, если ω = ω0, амплитуда вынужденного колебания по формулам (3.23) и (3.24) всегда является ограниченной.
Отметим, что при наличии затухания в системе с течением времени первые слагаемые (собственные колебания) формул (3.23) и (3.24) в силу затухания исчезают, остаются только чисто вынужденные колебания (третье слагаемое).
Для чисто вынужденных колебаний будем иметь
а) — без затухания
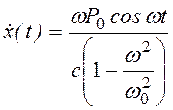 , (3.26)
, (3.26)
б) — с затуханием
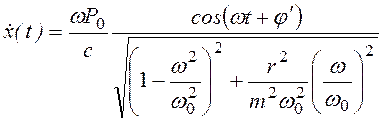 , (3.27)
, (3.27)
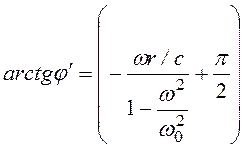 , (3.28)
, (3.28)
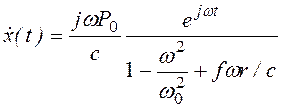 . (3.29)
. (3.29)
Диаграмма амплитуд и фаз в зависимости от коэффициента γ показана на рис. 3.27.
3.4. Динамические характеристики системы —
импеданс и адмитанс
Кривые на рис. 3.28 показывают, что при действии на систему периодической силы амплитуда колебаний зависит от частоты, что можно характеризовать как изменение с частотой сопротивления или податливости системы. Мерой указанных величин являются:
 |
|||||||
 |
|||||||
|
|||||||
|
|||||||
а) отношение силы к скорости вынужденного колебания - импеданс на основании формулы (3.24).
|
|
|||||||
|
||||||||
|
||||||||
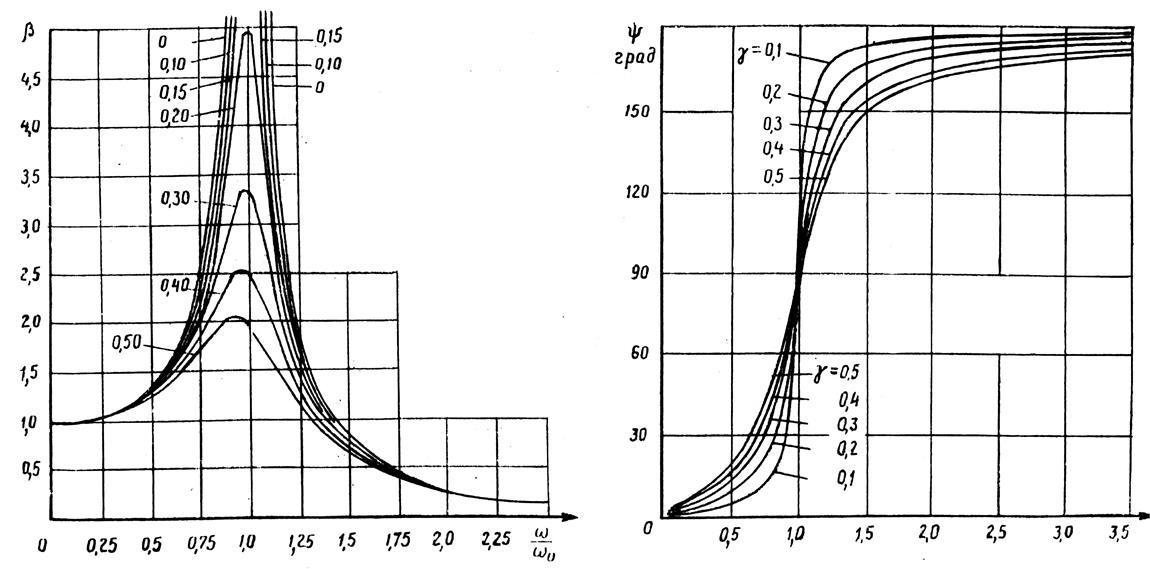
Рис. 3.27. Амплитудные кривые вынужденных колебаний и кривые фаз
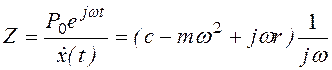 ; (3.30)
; (3.30)
б) обратная величина— отношение скорости вынужденного колебания к силе — адмитанс
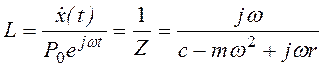 . (3.31)
. (3.31)
Эти величины являются функциями частоты и могут быть изображеныграфически. При наличии затухания эти величины комплексны и кривые, их изображающие, имеют пространственный характер (рис. 3.28 и 3.29). При отсутствии трения 6удем иметь
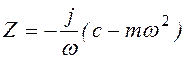 ,
, 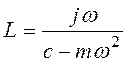 (3.32)
(3.32)
и плоские кривые. Множитель j указывает на то, что ординаты этих кривых сдвинуты по фазе относительно силы на 90°. Выражения
![]() ,
, 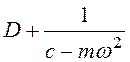 (3.33)
(3.33)
называются динамической жесткостью и, соответственно, динамической податливостью механической системы. Эти величины играют большую роль для расчетов и экспериментальных исследований колебательных систем.
3.5. Электрическая аналогия механических колебаний
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.