Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы - импеданс и адмитанс, страница 5

В выражениях (3.4) и (3.5) величина a — амплитуда колебаний, см; ω — угловая частота, рад/с;φ — начальная фаза, рад, соответствующая углу, образованному с одной из осей радиусом-вектором ОА в момент времени, принимаемый за начальный. Угловая частота φ, частота  f и период Т связаны соотношениями

,     ;

,    .

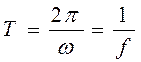В машиностроении часто приходится рассматривать число колебаний в минуту

п = 60f = 30ω/π = 9,55 ω кол.×мин.^-1.(3.6)

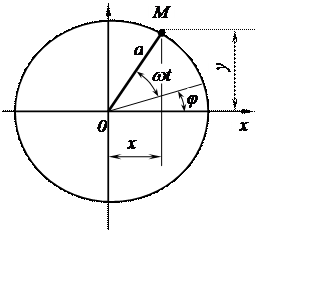
При рассмотрении на рис. 3.7 отрезка ОА как вектора, колебание можно выразить в комплексном вид

z= x+ jy= acos(ωt+φ) + jasin(ωt+φ) = ae^j(ωt+φ) = ae^jφ e^jωt,                                                                                                     (3.7)

где    ae^jφ - комплексная амплитуда.

 

Рис. 3.7. Круговое движение точки       Рис. 3.8. Сложение гармонических

                                                                                   колебаний

Два гармонических колебания ae^j(ω1+φ1) и ae^j(ω2t+φ2) складываются по закону сложения комплексных чисел при помощи векторной диаграммы (рис. 3.8).

При сложении двух гармонических колебаний одинакового (или различного) направления   следует   учесть, что вращение радиуса векторов ОА₁ и ОА₂ может   происходить в одну сторону или в разные стороны.

Если   ----- ω₂ = - ω₁= - ω,      φ₂= - φ₁,      a₁ = a₂ = a,

то суммарное колебание  представляет собой косинусоидальное движение вдоль оси, образующей с осью х угол φ,

z = ae^j(ωt+φ) + ae^-j(ωt+φ) = 2a cos(ωt+φ)                  (3.8)

При сложении гармонических колебаний одного направления с различными частотами ω₁ и ω₂ движение имеет выражение

z = a+a= 2acos (ω₁-ω₂)/2*         (3.9)

и представляет собой колебание с частотой, равной (ω₁+ω₂)/2, и амплитудой, изменяющейся периодически с частотой (ω₁-ω₂)/2. Если значения ω₁ и ω₂  близки между собой, то период T_II = 4π/(ω₁ - ω₂) велик по сравнению с периодом  Т_I= 4π/(ω₁+ω₂) (рис. 3.9); возникает явление, называемое биением.

Колебания, состоящие из нескольких гармонических колебаний различных частот, называются полигармоническими.

Каждое из слагаемых движений называется гармонической составляющей (гармоникой); совокупность значений частот колебаний гармоник, участвующих в общем движении, называется частотным спектром колебаний; отношение частоты гармоники к основной (первой) частоте называется порядком данной гармоники. Если совокупность частот слагаемых движений такова, что их значения образуют континуальное множество, т.е. располагаются сплошь на числовой прямой или на каком-нибудь ее отрезке, то спектр называется сплошным; интервал значений частот, соответствующий указанному отрезку, называют полосой спектра; ширина полосы равна длине отрезка. Колебания со сплошным спектром называют шумовыми колебаниями, или просто шумом.

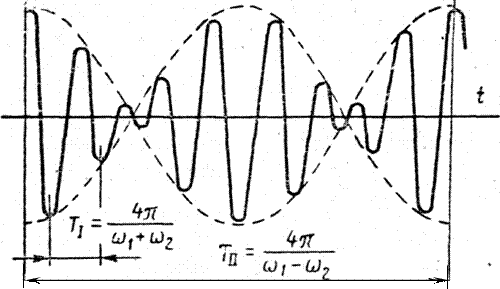
Рис. 3.9. Биения при сложении двух гармонических колебаний

На рис. 3.10  изображен процесс простого гармонического колебания.

 

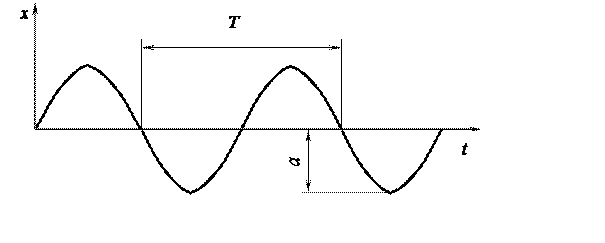Рис.  3.10. Гармоническое колебание

На рис. 3.11,а изображено шесть простых гармонических движений (одно из них — постоянное отклонение); при сложении этих движений получается суммарное движение, характеризующее некоторый колебательный процесс (рис. 3.11,б).

а)

 

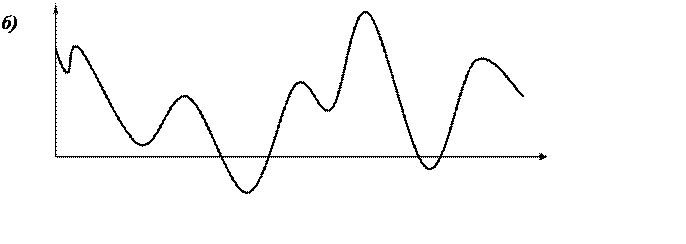Рис. 3.11. Гармонические составляющие

и составное колебательноедвижение

На рис. 3.12 изображено сложное движение в виде прямоугольного синуса. Это движение состоит из нескольких гармоник, однако, если сложить хотя бы три первые составляющие нечетного порядка (1-я, 3-я, 5-я), показанные на рис. 3.13, б, то можно получить движение, качественно и количественно приближающееся к данному (рис. 3.13,а).

 

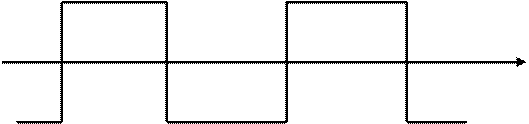Рис. 3.12. Движение по прямоугольному синусу

Процесс колебаний нередко происходит таким образом, что амплитуда, частота или фаза во времени периодически изменяется, причем период изменений достаточно велик по сравнению с периодом процесса. Такие колебания называются модулированными. В частности, колебание может происходить по закону