Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы - импеданс и адмитанс, страница 22

Изучение изгибных колебаний вращающегося вала начинается с рас-

смотрения движения сечения, в котором прикреплена деталь (диск). Это движение слагается из деформаций вала и его вращения.

Рассмотрим сначала движение по отношению к неподвижной системе координат xys, оси которой расположены так: ось x вертикальна и направлена вниз, ось у горизонтальна, ось s направлена к наблюдателю и совпадает с осью вала. Начало О координат расположено на линии опор. Вал будем считать вращающимся с постоянной угловой скоростью и против часовой стрелки.

Колебательные движения центра сечения характеризуются его перемещениями в направлении х и у, поворот сечения — углами поворота φ и d вокруг осей х и у (рис. 3.55). Колебательные движения центра и поворот сечения могут быть отнесены с деталями (диску), непосредственно связанной с этим сечением, если эту деталь считать, как это делается в большинстве случаев, абсолютно жесткой, т.е. недеформируемой.

б)

а)

S

            

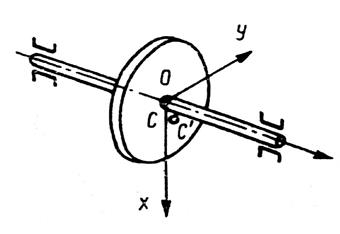
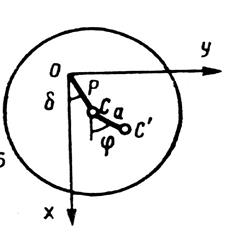
Рис. 3. 55. Гибкий вал с неуравновешенным диском

Если диск, прикрепленный к валу, неуравновешен (т.е. если центр тяжести диска не совпадает с центром сечения вала), то движение центра массы диска может быть представлено в виде движения концов суммы двух векторов: вектора , , характеризующего и неуравновешенность.

Движение удобно описывать с помощью комплексного представления векторов, а именно;

                                                                                                                   (3.86)

В простейших случаях приходится иметь дело с таким движением, при котором центр вала описывает эллипс, а вектор неуравновешенности вращается в плоскости с угловой  скоростью ω вала. В таких случаях движение центра массы описывается выражением

,                                                                                                                   (3.87)

где     U,  Vи λ — постоянные величины.

Геометрически такое движение представляется как сумма трех векторов постоянной длины (рис. 3.56), из которых два вращаются в противоположные стороны с угловой  скоростью λ, а третий с угловой скоростью ω вращения диска (вала). Если одна из постоянных величин Uили Vравна нулю, то движение будет слагаться из кругового движения центра вала и кругового движения вектора неуравновешенности.

			Круговое движение центра вала (или точки прикрепления диска) будем называть прецессией центра вала, λ — скоростью прецессии. Если V= 0, то прецессия выражается вектором Uи будет прямой; если U= 0, то прецессия выражается вектором Vи будет обратной. Выражение  представляет эллиптическое движение, которое можно называть обобщенной  прецессией.  Это  движение

 

будет прямым, если U> V, и обратным, если U < V.

В первом случае конец результирующего вектора (или что, та же точка на эллипсе) будет двигаться против часовой стрелки, во втором — по часовой стрелке.

Если в частном случае V =0 и λ = φ, т. е. скорость прямой прецессии равна скорости вращения диска вала, то движение можно представить выражением

.                                                                                                                   (3.88)

Прецессия есть результат сложения колебаний в двух взаимно перпендикулярных направлениях. Чтобы это наглядно представить, рассмотрим систему координат ξηsс началом точки О, вращающуюся вместе с валом с угловой скоростью ω. Оси этой системы будем ориентировать так, чтобы ось ξ была направлена вдоль вектора неуравновешенности.

Имеем такое преобразование  координат

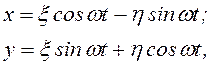                                                                                                                   (3.89)

где     ξ и h— прогибы вала в системе ξηs.