Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы - импеданс и адмитанс, страница 23

Умножив второе из соотношений (3.89) на  и сложив с первым, получим комплексное выражение соотношения вектора прогиба в неподвижной и подвижной системах координат

,                                                                                                                   (3.90)

и вместо (3.87) получим

.                                                                                                                   (3.91)

В принятой подвижной системе координат ξηs вал оказывается невращающимся, поэтому всякое движение центра вала или центра массы диска происходит только в результате упругих колебаний.

Если в уравнении (3.91) отделить вещественную часть от мнимой, то движение в подвижной системе координат будет выражаться следующим образом:

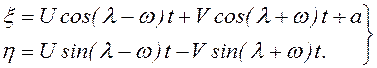.                                                                                                                   (3.92)

Следовательно, формула (3.91) выражает колебание вала, слагающееся из двух гармонических колебаний с угловыми частотами λ – ω и
λ + w. Таким образом, угловая частота колебаний есть то же, что и скорость прецессии в подвижной системе координат.

В случае прямой прецессии с угловой скоростью ω, выражаемой уравнением (3.90), частота колебаний будет ω – ω = 0 и вал будет иметь постоянный изгиб; такую прецессию назовем нулевой. При нулевой прецессии, следовательно, деформации вала не изменяются во времени.

Если отделить вещественную от мнимой части в выражении в неподвижной системе координат, то получаются проекции колебаний на неподвижные оси

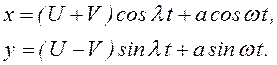                                                                                                                   (3.93)

Эти колебания представляют наложение колебаний с угловой частотой λ и с угловой частотой ω. Как видим, частота колебаний проекции точки на те или иные оси зависит от скорости вращения осей.

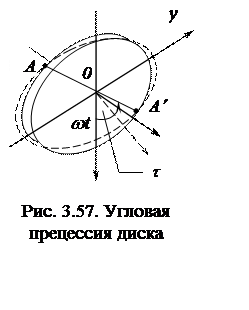
Если рассматривать колебания прикрепленного к валу диска, плоскость которого не точно перпендикулярна к оси вала, а имеет малое угловое отклонение τ, то увидим, что при вращении диска вокруг оси, совпадающей с осью вала, плоскость диска будет совершать движение так, что линия пересечения плоскости диска с плоскостью, перпендикулярной оси вала (линия узлов АА'), будет вращаться вокруг оси вала с угловой скоростью ω (рис. 3.57). Это движение назовем угловой прецессией диска.

Углы ψ и χ, образуемые плоскостью диска с осями x и y, в этом частном случае, т.е. при отсутствии угловых колебаний вала, выразятся так:

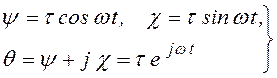.                        (3.94)

Если, кроме того, вал претерпевает изменяющийся во времени изгиб, в результате которого возникают малые наклоны его упругой линии относительно осей x и у, изменяющиеся по гармоническому  закону, то полные углы наклона ψ и χ, считая их также малыми, можно выразить так:

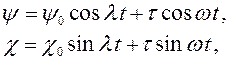
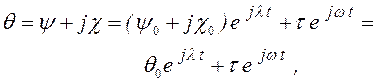                                                                                                                   (3.95)

где     ψ₀, χ₀, θ₀ — амплитудные значения соответствующих углов.

В более общем случае угловое прецессионное движение диска характеризует выражение

                                                                                                                   (3.96)

Очевидно, что вектор направлен по узловой линии и  вращается вместе с ней, характеризуя прецессионное движение. Модуль вектора θ, представляющий угол наклона оси диска к оси вала, и есть так называемый угол нутации.

При вращении узловой линии в сторону вращения вала будет иметь место прямая, при вращении линии узлов в сторону, обратную движению вала, – обратная угловая прецессия.

Если рассматривать движение в системе координат, вращающейся вместе с валом с угловой скоростью ω, то формулу (3.95) посредством соотношения

можно преобразовать в следующую:

.                                                                                                                   (3.97)

Частотаугловых колебаний диска равна скорости угловой прецессии.

3.14. Частоты собственных колебаний и критические скорости