Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы - импеданс и адмитанс, страница 14

Здесь ω_x и ω_θ — частоты собственных колебаний системы в случае, если один раз тело будет закреплено так, что не сможет поворачиваться, а в другой раз центр тяжести тела будет закреплен так, что не сможет перемещаться. Такие частоты называются парциальными частотами.

Собственные колебания системы в простейшем случае имеют общие выражения

,                                                                                                                      (3.49)

где     Xи θ суть амплитуды.

Подстановка выражений (3.49)в уравнения (3.48) приводит к двум   однородным уравнениям

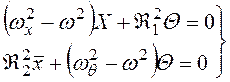,                                                                                                                   (3.50)

из которых получается алгебраическое уравнение частот связанных собственных колебаний системы

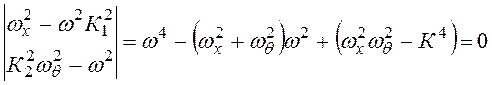.                                                                                                                   (3.51)

откуда получаются два значения квадрата частоты собственных колебаний системы  и .

Можно видеть, что парциальные  частоты ω_x и ω_θ всегда лежат внутри интервала между собственными частотами ω₁ и ω_2.

На рис. 3.37  изображены зависимости собственных частот ω₁ и ω₂ от соотношения ω_x и ω_θ, и от коэффициента , определяющего степень связанности системы. При  = 0 система не будет связанной и частоты собственных колебаний будут равны парциальным частотам.

Теперь можно выразить координаты х и θ в самом общем

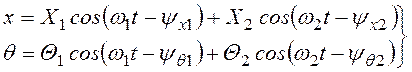.                                                                                                                   (3.52)

В выражениях (3.52) имеется восемь постоянных величин, в то время как начальных условий может быть только четыре. Но решение задачи имеет определенность при равенстве фаз , . В самом деле, из (3.50) можно получить

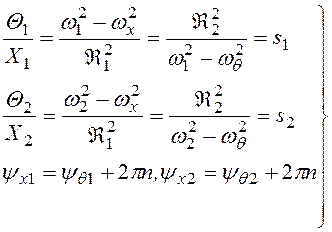,                                                                                                                   (3.53)

а отсюда  выражения (3.52) получают вид

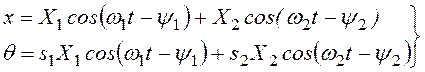                                                                                                                   (3.54)

1

2

1

0

2

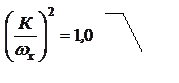
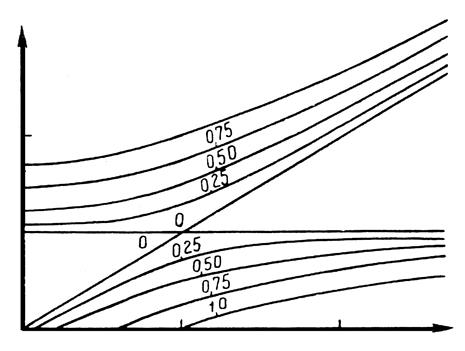
Рис. 3.37. Диаграмма зависимости частоты связанных колебаний

от парциальных частот и коэффициента связанности

Для начальных условий при t = 0, x = x₀, , ,  получим значение X₁ и X₂

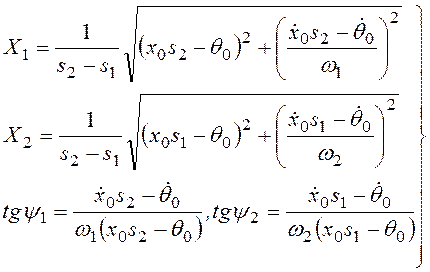                                                                                                                   (3.55)

Процесс колебаний, характеризующийся выражениями (3.54), является составным и состоит из двух гармонических колебаний с частотами ω₁ и ω₂. Можно выбрать такие начальные условия, чтобы колебания совершались только с одной частотой и были бы чисто гармоническими. Для этого нужно положить

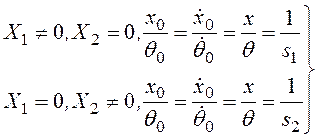.                                                                                                                   (3.55)

Тогда отношение величин х и θ будет сохранять постоянное значение; кроме того, будем иметь два типа движения, которые сводятся к поворотам тела относительно двух точек О₁ и О₂, соответствующих частотам ω₁ и ω₂. Учитывая малость угла θ , имеем для l_i (i = 1,2, рис. 3.38).

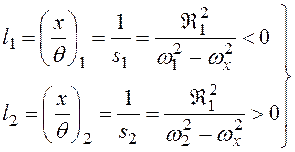.                                                                                                                   (3.56)

 

Рис. 3.38. Главные колебания

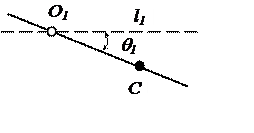Каждая из двух совокупностей значений (x, θ)₁, и (x, θ)₂, называется формой колебаний. Периоды колебаний 2π/ω₁ и 2π/ω₂ называются периодами главных колебаний; всякое собственное колебание системы является комбинацией из главных колебаний.