Механическая колебательная система и методы ее анализа. Кинематика колебаний и возбуждающие нагрузки. Динамические характеристики системы - импеданс и адмитанс, страница 27

.

Относительная скорость будет

.

Обратно, переходя к  неподвижной системе координат, будем иметь

на сновании чего можно выразить силу внутреннего   трения

                                                                                                                 (3.105)

где     r – коэффициентвнутреннего трения.

Итак, при учете внешнего и внутреннего трения дифференциальные уравнения колебаний вала с диском в середине будут иметь вид

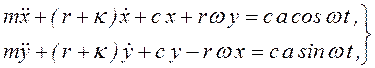                                                                                                                 (3.106)

где     r и к – коэффициенты внутреннего и внешнего трения.

Эти уравнения с помощью примененного ранее приема приводятся к одному комплексному уравнению

.                                                                                                                 (3.107)

Решение уравнения (3.107) имеет вид

,                                                                                                                  (3.108)

где     ω₁ + ja  и  –ω₁ + jβ –  комплексные корни квадратного уравнения

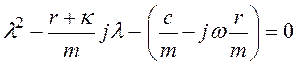;                                                                                                                 (3.109)

U и V– произвольные постоянные, зависящие от начальных условий движения, а величина Z определяется по формуле

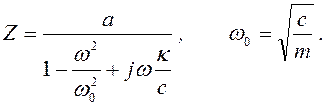                                                                                                                 (3.110)

Формула (3.108) для колебательного движения вала с учетом сил трения отличается от формулы (3.103) для колебательного движения вала без их учета следующим: частоты собственных колебаний, входящие в два первых члена, суть комплексные величины; амплитуда вынужденного кругового движения центра тяжести диска, определяемая третьим членом, выражение которого дано формулой (3.110), также комплексная.

Прежде всего, можно установить, что при  радиус кругового движения будет ограниченным. Разделяя вещественную и мнимую части, найдем радиус кругового движения

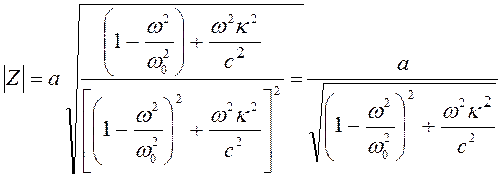                                                                                                                 (3.111)

и фаза между вектором дебаланса и вектором перемещения центра диска

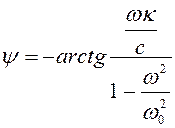.                                                                                                                 (3.112)

В частности, при ω = ω₀, т.е. при критической скорости, соответствующей идеальному (без трения) валу, фаза равна –π/2. Таким образом, в отличие от случая идеального вала вектор перемещения ОС и вектор дебаланса СС' не параллельны; фаза при изменении угловой скорости меняется непрерывно.

Кроме того, из формул (3.108) и (3.110) видно, что на вынужденное движение центра тяжести вала влияет лишь внешнее трение, внутреннее же трение не влияет, так как коэффициент r в эти формулы не входит. Поэтому, если положить r = 0, формулы будут такие же, как и без трения. Этот результат физически очевиден, так как при круговом движении центра тяжести и при постоянной конфигурации треугольника ОСС' вал не претерпевает переменных напряжений изгиба, а поэтому для такого движения внутреннее трение не имеет значения.

3.16. Консольный вал с диском

Особенностью колебаний консольного вала с диском является способность диска не только прогибаться, но и поворачиваться, что связано с возможностью поперечного (линейного) и углового перемещения концевого сечения вала. Для вывода дифференциальных уравнений изгиба такого вала (рис. 3.61) используем известные теоремы о количестве движения и моменте количеств движения.

Проекции на неподвижные оси x и у производной от количества движения диска будут равны проекциям на те же оси сил упругости, действующих со стороны вала

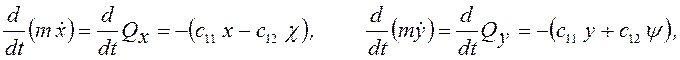                                                                                                                 (3.113)

где     χ и ψ – углы поворотов (малых) сечения вокруг осей у и х.

Проекции на те же оси производной от момента количества движения будут равны моментам сил упругости, действующим на диск со стороны вала.

Рис. 3.61. Консольный  вал