
Рис. 3.31. Амплитудная кривая нелинейной
системы
с жесткой характеристикой восстанавливающей
силы
На рис. 3.33 и 3.34 показаны
кривые изменения фаз соответственно рис. 3.31 и 3.32.
Следует отметить явление,
называемое скачком, присущее нелинейной системе. Для системы с амплитудной
кривой, изображенной на рис. 3.35, в случае весьма медленного увеличения частоты
вынужденных колебаний амплитуда будет расти от точки 1 до точки А, а
затем произойдет скачок вниз (срыв) с точки А в точку В, после
чего амплитуда пойдет понижней ветви кривой. При уменьшении частоты
вынужденных колебаний амплитуда будет расти до точки С, а затем в точке С
произойдет скачок вверх с точки С в точку D, после чего амплитуда пойдет по верхней ветви кривой до точки 1.

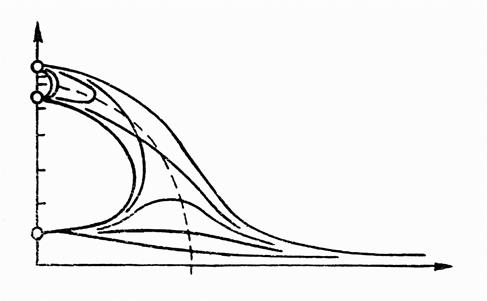
Рис. 3.32. Амплитудная кривая нелинейнойсистемы
с мягкой
характеристикой восстанавливающей силы
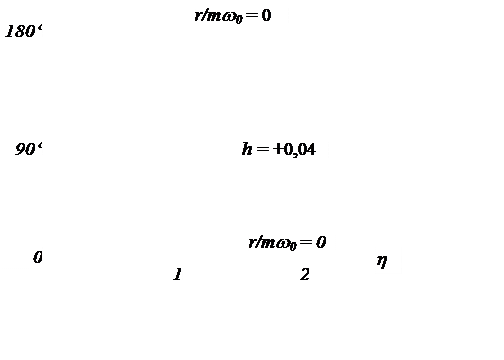
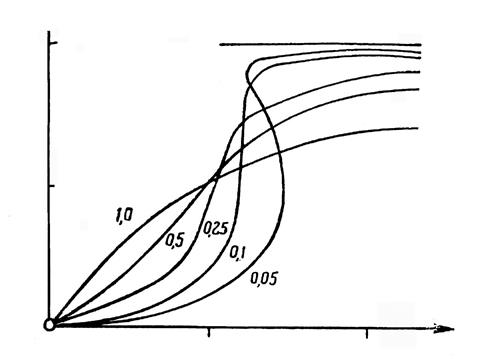
Рис. 3.33. Кривые
фаз нелинейной системы
с жесткой характеристикой восстанавливающей
силы
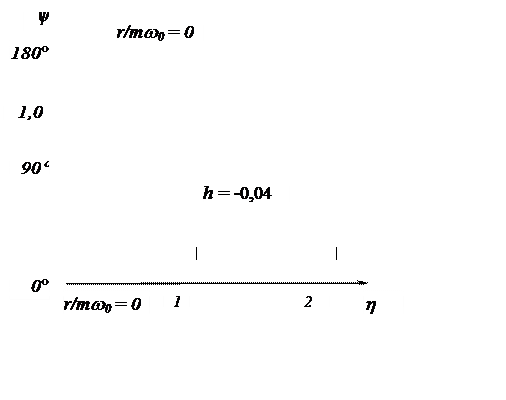
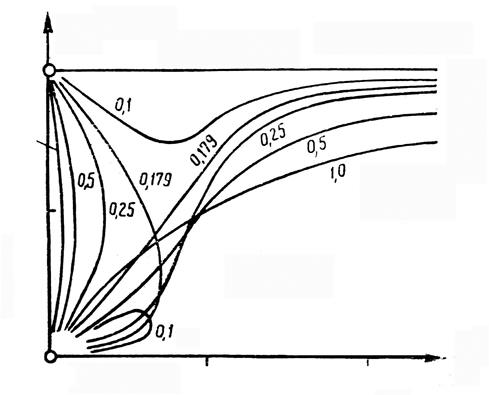
Рис. 3. 34. Кривые
фаз нелинейной системы
с мягкой характеристикой
восстанавливающей силы
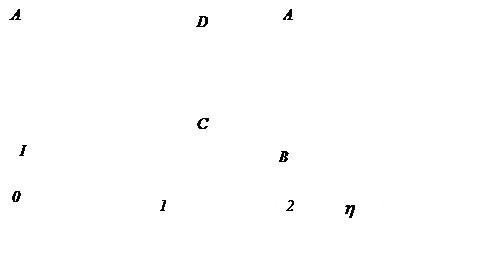
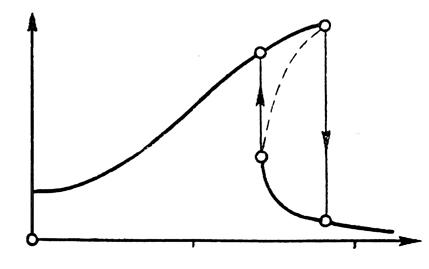
Рис. 3.35. Явление „скачка" в нелинейной
системе
3.7. Связанные колебания
систем с двумя степенями свободы
Большое число
машиностроительных конструкций может быть представлено в виде систем с
несколькими степенями свободы. Колебания таких систем имеют некоторые свойства,
которые; здесь будут рассмотрены. К таким свойствам относится в первую очередь
связанность колебаний отдельных частей или, как их называют, парциальных
систем. Системы с несколькими степенями свободы имеют главные координаты,
обладающие тем свойством, что, приняв их в качестве обобщенных координат, получаем
разделение системы на независимые части, совершающие самостоятельно
гармонические колебания. Эта глава является вводной к следующей главе, в
которой рассматриваются специальные методы анализа сложных колебательных
систем.
Рассмотрим пример связанных
собственных колебаний системы с двумя степенями свободы. Твердое тело,
подвешенное двумя пружинами на концах (рис. 3.36), способно совершать как
поступательные движения, так и повороты в плоскости, Примем в качестве
обобщенных координат следующие величины: перемещение х центра тяжести и
поворот θ тела. Кинетическая энергия тела и потенциальная энергия упруго
деформированных пружин будут иметь выражения соответственно
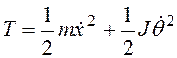 ,
, 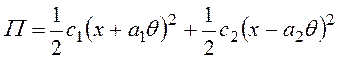 ,
,
где m – масса; J- момент
инерции тела.
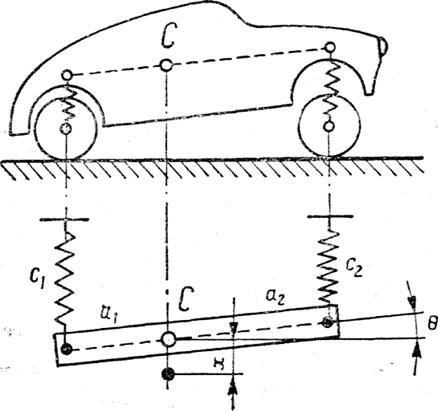
Рис. 3. 36.
Система с двумя степенями свободы
Вставив эти выражения в
дифференциальные уравнения Лагранжа, получим два дифференциальных уравнения
колебаний системы
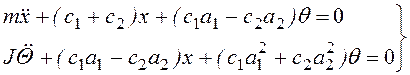 (3.47)
(3.47)
Вводя для упрощения
обозначения
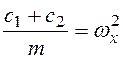 ,
, 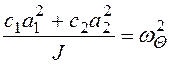 ,
, 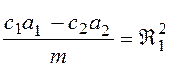 ,
,
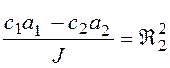 ,
, 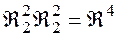 ,
,
получим дифференциальные уравнения
движения в сокращенной записи
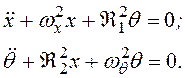 (3.48)
(3.48)








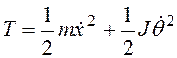 ,
, 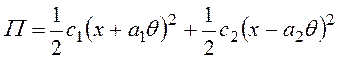 ,
,
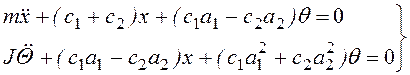 (3.47)
(3.47)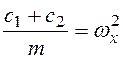 ,
, 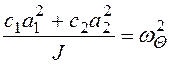 ,
, 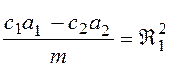 ,
,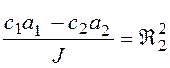 ,
, ![]() ,
,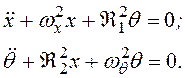 (3.48)
(3.48)