Одной из наиболее важных задач потенциометрии является определение концентрации и активности ионов водорода, а также определение констант кислотно-основного равновесия (рН-метрия).
При погружении электрода в среду (раствор или расплав), содержащую ионы, способные обмениваться с электродом, на границе раздела электрод-раствор возникает разность потенциалов, величина и знак которой однозначно определяются природой электрода, среды и внешними термодинамическими параметрами (температура, давление).
Рассмотрим равновесную систему, состоящую из металлического электрода и раствора, содержащего ионы этого металла Ме+n
Me/Me+n.
В металлическом электроде атомы металла находятся в равновесии с ионами и электронами. Это соответствует процессу
Разность электрических потенциалов между металлом и
раствором обозначается символом 
и называется электродным
потенциалом. Электродный потенциал Е является выражением меры стремления
положительных ионов перейти из металла в раствор.
Уравнение Нернста для зависимости электродного потенциала от активности ионов в растворе:
= 
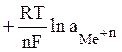. (2)
Здесь 
– активность ионов Me+n,
F – число Фарадея. называется
стандартным электродным потенциалом; эта величина равна электродному
потенциалу в стандартном состоянии (при 
= 1).
Хотя абсолютное значение определить
нельзя, это не создает трудности в практическом использовании уравнения
Нернста, так как в электрохимии принят способ отсчета стандартных потенциалов
от потенциала стандартного водородного электрода, который условно принят равным
нулю.
Система, состоящая из электрода, находящегося в равновесии с раствором, называется полуэлементом. Комбинация двух полуэлементов дает гальванический элемент.
Рассмотрим элемент следующего вида:
 |
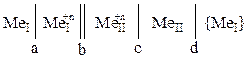(3)
Электродами в этом элементе являются металлы MeI и MeII. Для исключения контактной разности потенциалов при определении ЭДС элемента к правому электроду MeII присоединен токоотвод из MeI – {MeI}. Электродвижущая сила элемента (3) (ЭДС) будет определяться разностью электрических потенциалов между электродом MeI и токоотводом.
(Границы между твердыми фазами и между твердыми и жидкими фазами обозначаются одной вертикальной чертой, граница между жидкими фазами – двумя чертами.)
Электродная реакция, протекающая на левом электроде (граница а), может быть представлена уравнением
MeI ® ne (в MeI) + 
.
На правом электроде (граница с)
+ ne (в MeII)
®
MeII
.
На границе (d) между MeII и {MeI} происходит обмен электронами:
Уравнение Нернста для гальванического элемента:
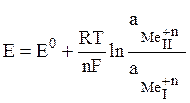, (4)
где ЭДС элемента (Е) равна разности электродных потенциалов
,
а стандартная ЭДС – разности стандартных электродных потенциалов
.
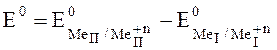Как мы уже отмечали выше, невозможность определить абсолютные значения электродного потенциала не создаёт неудобства в практическом использовании этой величины. В электрохимии принято отсчитывать значения потенциала от потенциала стандартного водородного электрода, представляющего собой полуэлемент следующего вида:
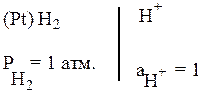
Электродный потенциал любого электрода принимается равным ЭДС элемента, составленного из исследуемого электрода и стандартного водородного электрода
 |
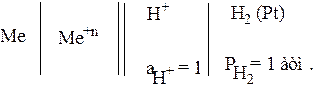(5)
Стандартный электродный потенциал равен ЭДС этого элемента при активности ионов металла, равной единице.
В тех случаях, когда водородный электрод по тем или иным причинам не может быть использован в качестве электрода сравнения, пользуются вспомогательными электродами сравнения, потенциал которых относительно водородного электрода точно известен и отличается большой устойчивостью.
В последнее время наиболее часто применяется хлорсеребряный электрод
Ag; AgCl | Cl–
Электродная реакция, протекающая на хлорсеребряном электроде:
Ag + Cl– – e ® AgCl
Зависимость потенциала от активности ионов хлора выражается уравнением:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.