Практикум по биохимии. Часть I. Физико-химические методы: Учебное пособие, страница 14

где k₁, k_-1 и k₂ – константы скорости соответствующих реакций.

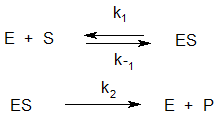
Наиболее медленной, лимитирующей скорость всего процесса, является стадия образования продукта реакции, поэтому начальная скорость реакции равна

v⁰  =  k₂[ES]                                                 (2)

Скорость накопления комплекса ES равна

d[ES]/dt  =  k₁[E] [S]  -  k_-1[ES]  -  k₂ [ES]              (3)

где первый член соответствует скорости образования фермент-субстратного комплекса, а второй и третий – скорости его распада.

Если обозначить общую концентрацию субстрата S, а общую концентрацию фермента Е₀, то уравнения баланса по субстрату и ферменту можно представить следующим образом:

S = [S] + [ES] + [P]                                   (4)

Е₀ = [ES] + [E]                                          (5)

Практически всегда концентрация субстрата намного больше концентрации фермента, т. е. S >> E₀. Следовательно, величиной [ES] по сравнению с [S] в уравнении (4) можно пренебречь. Поскольку мы определяем начальную скорость реакции, то концентрация продукта реакции [P] в этот момент времени близка к нулю. Тогда из уравнения (4) следует, что в начале реакции

[S] ≈ S                                                     (6)

Выражая из уравнения (5) концентрацию фермента, получим, что

[E] = E₀ – [ES]                                       (7)

Подставляя [S] и [E] из (6) и (7) в уравнение (3), получаем

d[ES]/dt  =  k₁(E₀ – [ES])S -  k_-1[ES]  -  k₂ [ES]

Поскольку ES является активной промежуточной частицей, его концентрацию можно считать квазистационарной, следовательно, скорость его накопления равна 0

k₁(E₀ – [ES])S -  k_-1[ES]  -  k₂ [ES]  =  0

Решая это уравнение относительно [ES], получаем

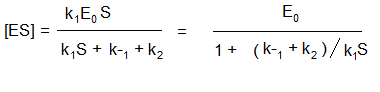
Подставляя значение [ES] в уравнение (2), получаем

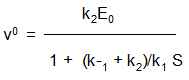
Выражение (k_-1 + k₂)/k₁ обозначим как К_m – константа Михаэлиса. Тогда начальная скорость ферментативной реакции равна

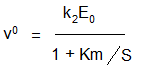
График зависимости v⁰ от S приведен на рис.1

 

Рис.1

Видно, что скорость реакции растет с ростом концентрации субстрата и при очень высоких концентрациях субстрата стремится к предельному значению k₂E₀, которое обозначают как V_max и называют максимальной скоростью реакции Отсюда получаем уравнение Михаэлиса

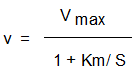
(Значок ⁰ у обозначения скорости обычно опускают, хотя следует помнить, что речь всегда идет о начальной скорости ферментативной реакции.)

Максимальная скорость реакции V_max = k₂E₀ зависит только от концентрации фермента и наблюдается при условии полного насыщения фермента субстратом (когда весь фермент находится в виде комплекса ES). При этих условиях дальнейшее увеличение концентрации субстрата не влияет на скорость реакции.

Из уравнения Михаэлиса вытекает, что при концентрации субстрата S, равной K_m, скорость реакции равна V_max/2. Таким образом, Константа Михаэлиса равна той концентрации субстрата, при которой скорость ферментативой реакции равна половине максимально возможной.

Зная параметры уравнения Михаэлиса K_m и V_max для данной реакции, можно рассчитать ее скорость при любой концентрации субстрата. Для определения этих параметров удобно воспользоваться обратными величинами скорости реакции и концентрации субстрата. Из уравнения Михаэлиса следует, что

1/v  =  1/V_max  +  K_m/V_max 1/S                         (8)

Отсюда видно, что график зависимости 1/v от 1/S представляет собой прямую

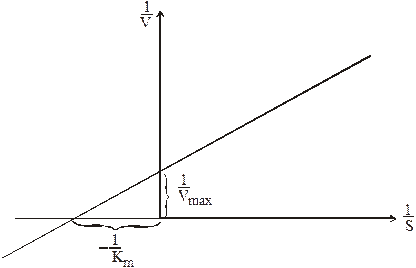
Рис.2

Из уравнения (8) следует, что отрезок, отсекаемый этой прямой на оси ординат, равен 1/V_max, а отрезок, отсекаемый ею на оси абсцисс, равен -1/ K_m. Это позволяет определить параметры уравнения Михаэлиса.

Ниже приведены две задачи по изучению кинетики реакций, одна из которых протекает без участия фермента и предполагает расчет констант скорости и энергии активации процесса, а другая, ферментативная, имеет целью определение величин K_m и V_max.

К-1. Кинетика гидролиза сахарозы

Приборы и реактивы

1.  Круговой спектрополяриметр

2.  Термостат               

3.  Секундомер                    

4.  Раствор 0,6 М HCl