Модель хроматографического процесса.Хотя используемые на практике методы хроматографии весьма различны по техническому исполнению, для всех методов характерна одна и та же хроматографическая ситуация, показанная на рис. 1. Имеется неподвижная фаза 2, способная растворять или адсорбировать исследуемые частицы, и фаза 1, называемая подвижной (газ или растворитель), которая перемещается относительно неподвижной фазы с некоторой линейной скоростью Uo (cм/сек). Наши частицы, являясь частью фазы 1, вынуждены перемещаться вместе с ней с той же скоростью uo.
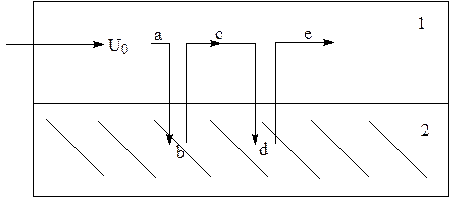
Рис. 1. В точках b и d молекула, сорбируясь в фазе 2, временно «выходит из игры».
Фазы 1 и 2 находятся обычно в высокодисперсном состоянии для обеспечения максимального контакта между ними, однако для понимания механизма процесса это обстоятельство несущественно, и можно рассматривать гипотетическую плоскую границу раздела, как показано на рис. 1.
Наконец, удобно отвлечься пока от конкретной геометрической формы хроматографической системы. Показанная на рис. 1 модель может быть колонкой, ось которой совпадает с вектором скорости Uо, пластинкой и т.д. В принципе, хроматография может быть одномерной, двухмерной или трехмерной. Мы будем рассматривать наиболее простой одномерный случай.
Скорость движения хроматографической зоны. Рассмотрим траекторию abcde некоторой «средней» частицы (рис. 1). Частица движется в фазе 1 по пути а до тех пор, пока не поглотится фазой 2. Среднее время «жизни» ее в неподвижной фазе равно t2. Затем она возвращается в фазу 1 и перемещается с ней со скоростью Uo на отрезке с в течение времени t1 до поглощения в точке d.
В точках b и d частица, «выбывая из игры», не участвует в движении со скоростью Uo; в результате средняя скорость продвижения частицы в фазе 1 равна некоторому значению U, которое ограничено пределами
O £ U £ Uo (5)
Из этого качественного рассмотрения видно, что в нашей модели U может зависеть только от Uo и соотношения времен t1 и t2. Крайние случаи неравенства (5) реализуются, когда частицы вообще не поглощаются фазой 2 (U = Uo), и когда взаимодействие частицы с фазой 2 настолько велико, что частица, поглотившись фазой 2, остается в ней навсегда (U = 0). Величина U называется скоростью движения хроматографической зоны.
Количественное рассмотрение. Рассмотрим слой хроматографической зоны толщиной dx на расстоянии х от начала движения (рис. 2).
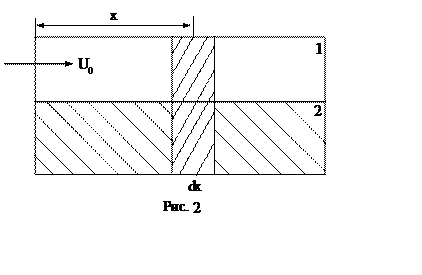

Двигаясь со средней скоростью U, зона компонента проходит этот путь за время 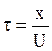 .
.
Примем далее, что на пути х частица испытала n актов поглощения – выделения, причем n достаточно велико, чтобы можно было говорить о «среднем» поведении частицы. В течение времени t частица пребывала в фазе 1 nt1 сек., а в фазе 2 – nt2 сек., причем nt1 + nt2= t. Средняя скорость частицы
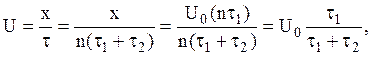 (6)
(6)
поскольку фактически путь x = Uo(nt1) частица прошла в фазе 1 за время nt1, двигаясь со скоростью Uo.
Отношение объемов фаз 1 и 2 связано с площадями их сечения S1 и S2 следующим образом:
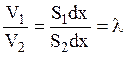 (7)
(7)
Используя формулу (7), выразим t1/t2 из уравнения (4):
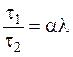 (8)
(8)
Подставляя (8) в (6), получаем уравнение скорости движения хроматографической зоны
U = U0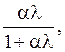 (9)
(9)
удовлетворяющее очевидным пределам (5).
График зависимости скорости движения частиц от коэффициента распределения α, показанный на рис. 3, используется для прямого экспериментального определения коэффициентов распределения a и идентификации пиков.
|

Если хроматографируется смесь молекул, частицы с различными значениями a перемещаются с разными скоростями U(a), в результате чего зоны компонентов разделяются, что используют для анализа и препаративного разделения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.