Методико-практический путеводитель по темам курса "Теория статистики", страница 31

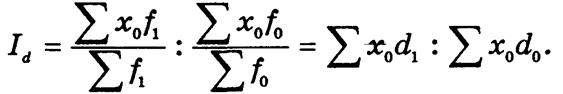
Формулы индексов фиксированного состава и структурных сдвигов разновзвешенные. В I_x веса фиксируются на уровне текущего периода, а в I_d значения признака х — на уровне базисного периода. Такой принцип взвешивания обеспечивает увязку трех индексов в систему

Пример. Определим индексы среднего размера страхового тарифа при страховании легковых автомобилей со сроком эксплуатации до 3 лет.

Таблица 8.3

Автомобиль	Страховой тариф, %		Страховая сумма, тыс. ден. ед.		Сумма страхового возмещения, тыс. ден. ед.
	Базис­ный перио x0	Теку­щий период x1	Базис­ный период f0	Теку­щий период f1	x0f0	x1f1	x0f1
Отечественный	2,5	3,0	520	750	13,0	22,5	18,75
Зарубежный	5,0	6,0	380	850	19,0	51,0	42,50
Итого	X	X	900	1600	32,0	73,5	61,25

Индекс переменного состава

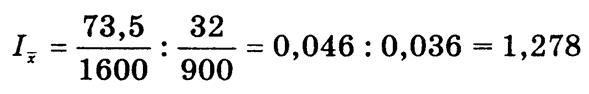
и показывает, что средний страховой тариф в текущем периоде по сравнению с базисным повысился на 27,8%. Индекс фиксированного состава

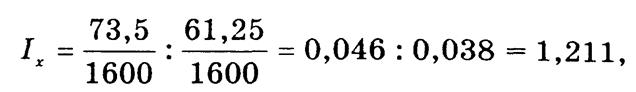
т.е. за счет повышения страхового тарифа по каждой группе автомобилей средний страховой тариф увеличился на 21,1%. Индекс структурных сдвигов I_d = 0,038 : 0,036 = 1,056, следовательно, средний страховой тариф повысился на 5,6% за счет изменения в составе объектов страхования, а именно — увеличения доли страховой суммы зарубежных автомобилей с более высокой страховой ставкой.

Взаимосвязь сопряженных индексов обеспечивается:

 = 1,211 • 1,056 = 1,278.

Разновидностью индексов средних величин являются территориальные индексы, в которых средние уровни сопоставляются по отдельным территориям, объектам.

Для построения территориальных индексов необходимо обосновать базу сравнения и порядок фиксации в пространстве значений признака х_j и структуры совокупности d_j. База сравнения может быть разной — для каждого объекта "своя" (она выбирается произвольно, в зависимости от цели сравнения) — либо одинаковой (средний уровень, стандарт). Например, при сравнении уровня смертности населения отдельных стран за стандарт принимается европейская возрастная структура населения. Средняя база для значений признака х_j определяется как средняя арифметическая взвешенная по двум объектам, а средняя структура — как структура суммарной по двум объектам совокупности.

Территориальный индекс переменного состава по объектам А и В вычисляется по формуле

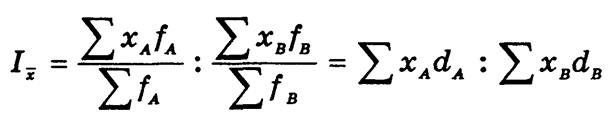
и показывает, во сколько раз средний уровень признака объекта А больше или меньше, чем объекта В.

Территориальный индекс фиксированного состава

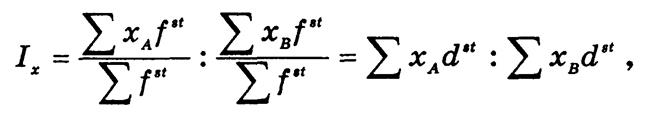
где f^st — частота; d^st — частость стандартной структуры совокупности. Вместо стандартной структуры совокупности может использоваться средняя структура. I_x показывает соотношение средних значений признака при фиксированной структуре совокупности.

Пример. Расчет территориальных индексов средней ожидаемой продолжительности жизни населения двух стран показан в табл. 8.4.

Таблица 8.4

Группа населения	Средняя ожидаемая продолжительность жизни, лет		Структура населения по полу, %
	Страна А хA	Страна В xb	Страна А dA	Страна В dB	Стандартная dst
Мужчины	72	62	46	52	49
Женщины	78	65	54	48	51
Итого	X	X	100	100	100

Территориальный индекс переменного состава  = (72 х 0,46 + 78 • 0,54) : (62 • 0,52 + 65 • 0,48) = 75,24 : 63,44 = 1,186. Следовательно, средняя ожидаемая продолжительность жизни населения страны А в 1,186 раза больше, чем в стране В.

Индекс фиксированного состава по стандартной структуре I_x = (72 • 0,49 + 78 • 0,51): (62 • 0,49 + 65 • 0,51) = 75,06 : 63,53 = 1,181.

Таким образом, при условии, что структура населения в обеих странах стандартная, средняя ожидаемая продолжительность жизни в стране А превышает уровень страны В на 18,1%.