Методико-практический путеводитель по темам курса "Теория статистики", страница 24

Значение коэффициента ранговой корреляции свидетельствует о наличии прямой и достаточно заветной связи между указанными параметрами риска иностранного инвестирования экономики. По прил. 6 критическое значение коэффициента ранговой коррекции для а = 0-05 и n = 7 составляет r_0,95(7) = 0,71, что значительно меньше фактического. Следовательно, существенность связи доказана с вероятностью 0,95.

Таблица 6.4

Страна	Интегральные показатели		Ранги показателей		Отклоне­ние рангов dj
	эффективности экономики (max = 10)	надежности делового партнерства (max = 100)	Rx	Ry		d2j
А	5,9	54.9	6	7	-1	1
В	7,1	54,8	7	6	1	1
С	4,2	45,3	4	5	-1	1
D	3,4	36,9	3	4	-1	1
К	4,9	35,8	5	3	2	4
М	2,7	26,4	1	2	-1	1
Р	2,9	24,8	2	1	1	1
Итого	X	X	X	X	0	10

Анализ взаимосвязей между атрибутивными признаками проводится на основе таблиц взаимной сопряженности (взаимозависимости), описывающих комбинационные распределения совокупностей по двум признакам — факторному х и результативному у. При наличии стохастической связи условные распределения изменяются от группы к группе. Оценка тесноты стохастической связи основывается на отклонениях частот (частостей) условных распределений от безусловного, т.е. на отклонениях фактических частот f_ij от теоретических F_ij, пропорциональных итоговым частотам безусловного распределения:

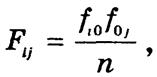
где f_i0 — итоговые частоты по признаку х; f_0j — итоговые частоты по признаку у, n — объем совокупности.

Очевидно, что

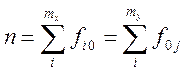
Абсолютную величину отклонений (f_ij - F_ij) характеризует квадратическая сопряженность Пирсона c²:

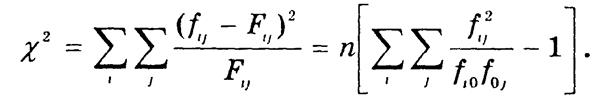
Если стохастическая связь отсутствует, то c² = 0. Для того, итобы сделать вывод о существенности связи, необходимо сравнить фактическое значение c² с критическим для заданной вероятности 1 - a и числа степеней свободы k = (m_x — 1)(m_y - 1), где m_x и m_y — соответственно количество групп по признакам х и у. Критические значения c² приведены в прил. 3.

Относительной мерой тесноты стохастической связи служат коэффициенты взаимной сопряженности С, которые по содержанию идентичны коэффициентам корреляции. Если m_x = m_y, используют коэффициент сопряженности Чупрова:

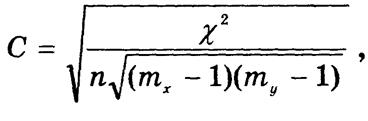
если m_x ¹ m_y, предпочтение отдают коэффициенту сопряженности Крамера:

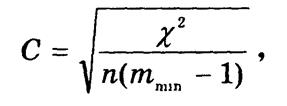
где m_min — минимальное количество групп по признаку х или у.

Значения коэффициента С колеблются в пределах от 0 до 1.

Пример. В табл. 6.5 приведено комбинационное распределение респондентов как потенциальных инвесторов по возрасту и склонности к риску. К группе рискующих отнесены респонденты, имеющие намерение приобрести ценные бумаги, несмотря на риск, осторожные не рискуют без гарантий, нерискующие избегают риска вообще. Концентрация частот около диагонали из верхнего левого угла в правый нижний свидетельствует о наличии стохастической связи. Фактическое значение c² составляет

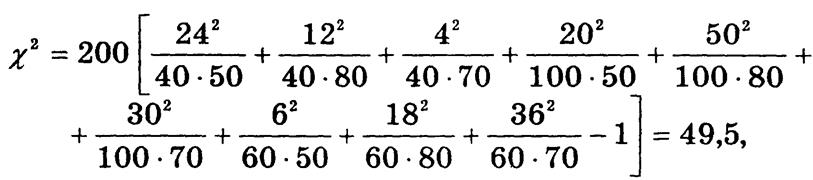
что значительно выше критического c²_0,95 (4) = 9,49. Следовательно, существенность связи между возрастом респондентов и склонностью их к риску доказана с вероятностью 0,95.

Таблица 6.5

Возраст, лет	Тип инвестора			Итого
	рискующий	осторожный	нерискующий
До 30	24	12	4	40
30—50	20	50	30	100
50 и старше	6	18	36	60
Итого	50	80	70	200

Поскольку m_x = m_y =3, для оценки тесноты связи используем коэффициент взаимной сопряженности Чупрова: