Методико-практический путеводитель по темам курса "Теория статистики", страница 19

При малых выборках (n < 30) квантиль t определяют по распределению вероятностей Стьюдента. В прил. 2 приведены значения t для F(x) = 0,95 и числа степеней свободы k= n - 1.

Пример. По данным анализа плавки легированной стали (10 проб), содержание никеля составляет в среднем 4,25% при s² = 0,18. Предельная ошибка выборки с вероятностью F(x) = 0,95, для которой  (9) = 2,26:

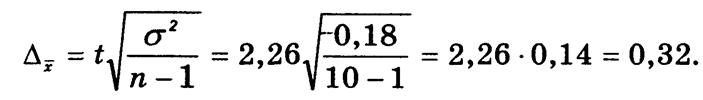
Доверительные границы: 4,25 ± 0,32, т.е. с вероятностью 0,95 можно утверждать, что содержание никеля в легированной стали не меньше 3,93 и не больше 4,57%.

При сравнении точности выборочных оценок используют относительную ошибку выборки V_m, которая показывает, на сколько процентов выборочная оценка отклоняется от параметра генеральной совокупности:

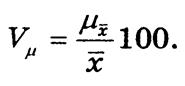
В нашем примере m = 0,14, а

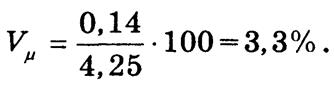
Относительную ошибку выборки можно рассчитывать на основе коэффициента вариации признака V_х:

для повторной выборки

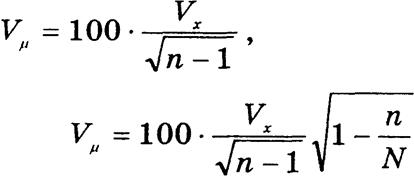
для бесповторной выборки.

Так, коэффициент вариации содержания никеля в легированной стали составит

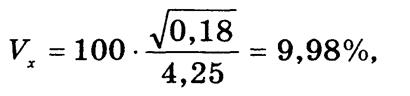
следовательно,

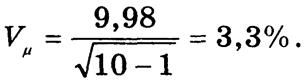
Аналогично рассчитывают относительную ошибку выборки для доли:

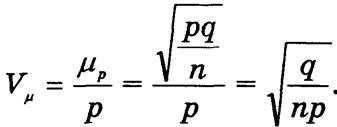
В практике выборочных обследований используют разные способы формирования выборочных совокупностей, в частности: простой случайный, механический, типический (районированный), серийный.

Простой случайный отбор проводится путем жеребьевки или на основе таблиц случайных чисел. Это классический способ формирования выборочной совокупности, и именно на нем основывается теория выборочного метода.

При механическом отборе основой выборки является упорядоченная численность элементов генеральной совокупности. Отбор элементов осуществляется через одинаковые интервалы, шаг интервала зависит от доли выборки. Так, при = 0,05 шаг интервала составляет 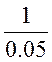 = 20. Ошибка механической выборки вычисляется по формуле бесповторной выборки. Для моментных наблюдений, фиксирующих состояние непрерывного процесса на определенные моменты времени, используют формулу ошибки повторной выборки.

Типический (районированный) отбор предусматривает предварительную структуризацию генеральной совокупности и независимый отбор элементов в каждой составной части. Объем типической выборки — это сумма частных выборок n_j, т. е. 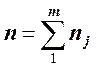 , где m — число составных частей (групп, типических районов и т. п.).

При вычислении ошибки типической выборки используют среднюю из групповых дисперсий

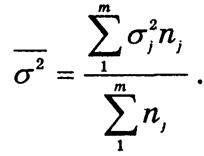
Как правило, , следовательно, ошибка типической выборки меньше, чем механической или простой случайной. Чаще всего используют отбор, пропорциональный численности составляющих совокупности, т. е. доля выборки для всех составляющих одинакова.

При серийном отборе основа выборки состоит из серий элементов совокупности, связанных территориально (районы, поселки), организационно (фирмы, акционерные общества) и т. п. Серии отбираются по схеме механической или простой случайной выборки, обследованию подлежат все элементы серии. При вычислении ошибки выборки учитывается межсерийная вариация:

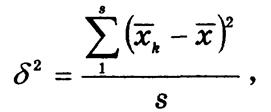
где s — число серий,  — средняя k-й серии.

Проектируя выборочные наблюдения, определяют минимально достаточный объем выборки, при котором выборочные оценки представляли бы основные свойства генеральной совокупности:

для повторного отбора

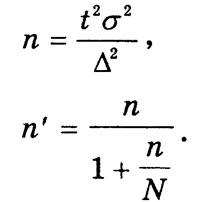
для бесповторного

Для определения объема выборки n используют оценки дисперсий s² аналогичных или пробных обследований. Если такие обследования отсутствуют, можно воспользоваться соотношением 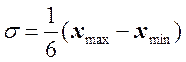, а для доли взять наибольшее значение дисперсии s² = 0,25.

Пример. Изучается отношение сельского населения региона к праву купли-продажи земли. По результатам аналогичных обследований в других регионах, 40% опрошенных поддерживают это право. При каком объеме выборки предельная ошибка (с вероятностью 0,954) не превысит 5%?

Опираясь на результаты аналогичных обследований, определим s2 = pq = 0,4 • 0,6 = 0,24. Тогда минимальный достаточный объем выборки составит

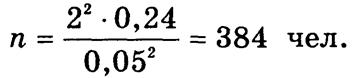
Если в основу расчета л положить относительную ошибку выборки V_D = tV_m формулы соответственно модифицируются:

для средней

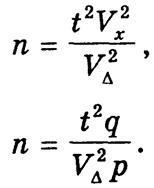
для доли