Методико-практический путеводитель по темам курса "Теория статистики", страница 20

Статистическая гипотеза — это определенное предположение относительно свойств генеральной совокупности, которое можно проверить по данным выборочного наблюдения. Гипотеза, которую необходимо проверить, формулируется как отсутствие различий между параметром генеральной совокупности G и заданной величиной а (нулевая гипотеза). Содержание ее записывают так: Н₀ :G = а. Каждой нулевой гипотезе противопоставляют альтернативную Н_а. В зависимости от значимости отклонений она формулируется как Н_а : G > а; Н_а : G < а или Н₀ : G ¹ а.

Если выборочные данные противоречат гипотезе Н₀ она отклоняется, если согласовываются с ней — Н₀ не отклоняется. Проверка гипотез непременно связана с риском принятия ошибочного решения: риск I рода — отклонение верной нулевой гипотезы, риск II рода — принятие Н₀ когда в действительности верна альтернативная.

Правило, по которому гипотеза Н₀ отклоняется или не отклоняется, называют статистическим критерием. Математической основой любого критерия является статистическая характеристика Z, закон распределения которой известен (например, характеристика t-распределения Стьюдента).

Вероятность риска отклонить верную гипотезу называют уровнем значимости а, а значение статистической характеристики для вероятности 1 - а — критическим значением Z_1-а. В приложении приведены критические значения наиболее распространенных статистических критериев. Если выборочное значение Z > Z^_1-а, гипотеза Н₀ отклоняется, при Z < Z_1-а не отклоняется.

В случае проверки справедливости Н₀ : G = а против Н₀ : G ¹ а используют двусторонний критерий, а критическое значение Z определяется для а/2 , т. е.

Пример/ На курсах восточных языков используют две методики обучения — новую и традиционную. Для сравнения эффективности новой методики проведено тестирование двух групп китайского языка по 100-балльной системе. Восемь слушателей, обучавшихся по новой методике, получили

средний бал  = 84 при дисперсии  = 32; 10 слушателей, обучавшихся по традиционной методике, за такой же тест имели средний балл  = 76 при дисперсии  = 24. Разность между средними двух групп составляет ( - ) = 84 - 76 = 8 баллов. Необходимо проверить, случайны ли эти различия, или они обусловлены большей эффективностью новой методики. Нулевая гипотеза формулируется, исходя из предположения, что отклонение средних случайно, т.е. Н₀ :  = . Альтернативная гипотеза предусматривает, что новая методика эффективнее, т. е. Н_a :  > . При таком формулировании H_a проводится односторонняя проверка нулевой гипотезы. Статистической характеристикой проверки H₀ является нормированное отклонение средних

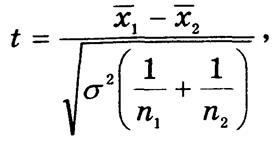
подчиненное распределению вероятностей Стьюдента с числом степеней, свободы k = n₁ + n₂ - 2.

В нашем примере k = 8 + 10 - 2 = 16; оценка средней из групповых дисперсий составляет:

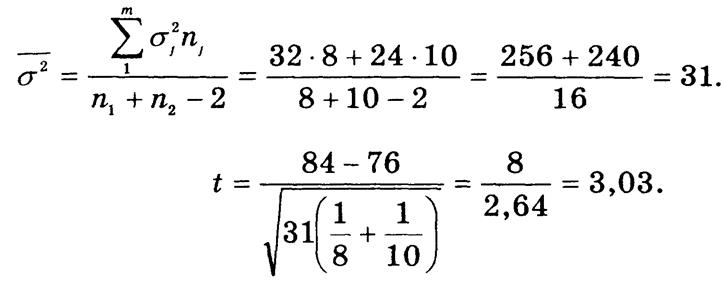
Критическое значение одностороннего t-критерия при а = 0,05 и k = 16 составляет t_0,95 (16) = 1,75, что меньше фактического (t = 3,03). Следовательно, нулевая гипотеза Н₀ :  =  отклоняется. С вероятностью 0,95 можно утверждать, что новая методика изучения восточных языков эффективнее.

6. Методы анализа взаимосвязей

Все социально-экономические явления взаимосвязаны. Связь между ними имеет причинно-следственный характер. Признаки, характеризующие причины и условия связи, называются факторными х, а признаки, которые характеризуют следствия связи, — результативными у. Между признаками х и у возникают разные по природе и характеру связи, а именно: функциональные и стохастические. При функциональной связи каждому значению признака х соответствует одно определенное значение у. Эта связь проявляется однозначно в каждом отдельном случае. При стохастической связи каждому значению признака х соответствует определенное множество значений y, образующих так называемое условное распределение. Как закон эта связь проявляется только в массе случаев и характеризуется изменением условных распределений у. Если заменить условное распределение средней величиной , то образуется разновидность стохастической связи — корреляционная. В случае корреляционной связи каждому значению признака х соответствует среднее значение результативного признака .