Методико-практический путеводитель по темам курса "Теория статистики", страница 16

Обобщающей мерой вариации является среднее отклонение индивидуальных значений признака от центра распределения. Поскольку алгебраическая сумма отклонений 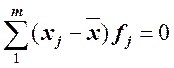, то в расчетах используют модули  или 1 квадраты  отклонений. Средний из модулей отклонений называют средним линейным отклонением ; средний квадрат отклонений — дисперсией s², корень квадратный из дисперсии — средним, квадратическим отклонением s:

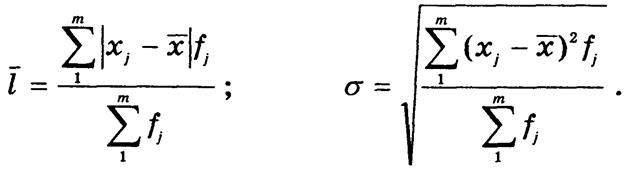
По первичным, несгруппированным данным приведенные характеристики вариации рассчитываются по принципу невзвешенной средней, т. е.:

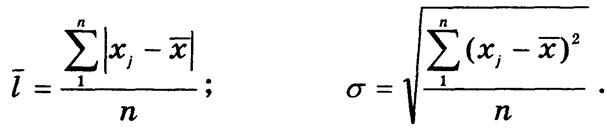
Среднее линейное и среднее квадратическое отклонения — именованные числа (в единицах измерения признака). По содержанию они идентичны, однако из-за математических свойств s > . В симметричном, близком к нормальному, распределении s = 1,25, R = 6s=  ± 3s.

Дисперсию используют не только для оценки вариации, но и при измерении взаимосвязей, для проверки статистических гипотез и т.п. Для признаков метрической шкалы расчет дисперсии ведется по формуле

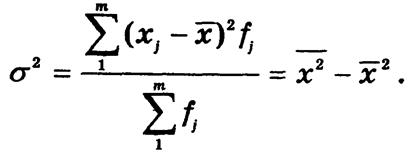
Как и любая средняя, дисперсия имеет определенные математические свойства:

а) если все значения признака х_j уменьшить (увеличить) на определенную величину, дисперсия не изменится;

б) если все значения признака изменить в k раз, то дисперсия изменится в k² раз;

в) в случае замены частот частостями дисперсия не изменится.

Для альтернативного признака, вариация которого имеет два взаимоисключающих значения — "1" и "0", а распределение характеризуется соответственно двумя частостями — d₁ и d₀, дисперсия рассчитывается как произведение частостей s² = d₁d₀ = d₁ (1 –d₁).

В табл. 4.2 показан расчет абсолютных характеристик вариации на примере срока обращения облигаций.

Таблица 4.2

Срок обращения облигаций, мес.	f	xj	xj - x	f	f
До 2	15	1	-4,6	69,0	317,40
2—4	13	3	-2,6	33,8	87,88
4—6	29	5	-0,6	17,4	10,44
6—8	22	7	1,4	30,8	43,12
8—10	12	9	3,4	40,8	138,72
10 и более	9	11	5,4	48,6	262,44
Итого	100	X	X	240,4	860,00

Средний срок обращения облигаций — 5,6 мес.; среднее линейное отклонение составляет  = 240,4 : 100 =2,4 мес.; дисперсия — s² = 860 : 100 = 8,6; среднее квадратическое отклонение — s =  = 2,9 мес.

Доля облигаций со сроком обращения менее 2 мес. составляет d₁ = 0,15. Дисперсия доли s² = 0,15 • (1 - 0,15) = 0,1275.

При сравнении вариаций разных признаков или одного признака в разных совокупностях, используют относительные характеристики вариации. Коэффициенты вариации рассчитываются как отношение абсолютных, именованных характеристик вариации (s, , R) к центру распределения и часто выражаются в процентах, следовательно:

1) линейный коэффициент вариации

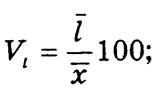
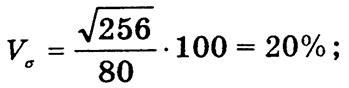
Коэффициент локализации рассчитывается для каждой j-й составляющей совокупности. При равномерном распределении все значения L_j = 1. В случае концентрации значении признака в j-й составляющей L_j > 1, и наоборот.

Коэффициент концентрации является обобщающей характеристикой отклонения распределения от равномерного. Значения его колеблются в пределах от 0 до 1. В равномерном распределении К = 0. Чем заметнее концентрация, тем больше значение К отклоняется от 0. Расчет коэффициентов L_j и к представлен в табл. 4.3 на примере распределения фермерских хозяйств по стоимости реализованной продукции.

Коэффициент концентрации составляет

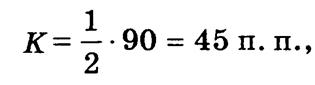
что свидетельствует об относительно высоком уровне концентрации товарного сельскохозяйственного производства в фермерских хозяйствах. Объемы товарной продукции концентрируются в крупных хозяйствах — в последней группе L_j = 8,00.

Таблица 4.3